Đề ôn tập và kiểm tra giữa học kì I toán 11 cấu trúc mới mới nhất

Câu 1 (1đ):

Cho dãy số có các số hạng đầu là $\dfrac13; \, \dfrac{1}{3^2}; \, \dfrac{1}{3^3}; \, \dfrac{1}{3^4};...$ . Số hạng tổng quát của dãy số này là

\dfrac{1}{3^{n-1}}

\dfrac{1}{3^{n}}

.

\dfrac{1}{3^{n+1}}

.

\dfrac{1}{3^{n+2}}

.

Câu 2 (1đ):

Dãy số nào sau đây là cấp số cộng?

u_n=2^{n+1}

.

u_n=(-3)^{n+1}

.

u_n=3^n

.

u_n=3n+1

.

Câu 3 (1đ):

Phương trình $\cot x=3$ có nghiệm là

x=arc\cot 3+k\pi, \, k\in \mathbb{Z}

.

x=arc\cot 3+k2\pi, \, k\in \mathbb{Z}

.

x=\cot 3+k2\pi, \, k\in \mathbb{Z}

.

x=\cot 3+k\pi, \, k\in \mathbb{Z}

.

Câu 4 (1đ):

Giá trị lớn nhất của hàm số $y=3\sin x$ là

3

.

-3

.

2

.

1

.

Câu 5 (1đ):

Đường cong hình bên dưới là đồ thị của hàm số nào trong bốn hàm số sau?

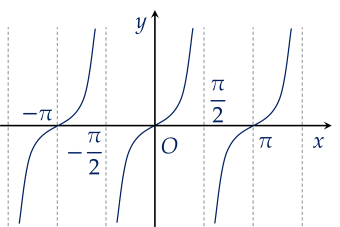
loading...

y=\cos x

.

y=\cot x

.

y=\tan x

.

y=\sin x

.

Câu 6 (1đ):

Khẳng định nào sau đây đúng?

Hàm số

y=\cos x

là hàm số lẻ.

Hàm số

y=\sin x

là hàm số chẵn.

Hàm số

y=\cot x

là hàm số chẵn.

Hàm số

y=\tan x

là hàm số lẻ.

Câu 7 (1đ):

Cho góc lượng giác $\left(OA,OB \right)$ có số đo bằng $\dfrac{\pi }{5}$ . Số nào sau đây là số đo của một góc lượng giác có cùng tia đầu, tia cuối với $\left(OA,OB \right)$ ?

\dfrac{6\pi }{5}.

\dfrac{31\pi }{5}.

\dfrac{9\pi }{5}.

-\dfrac{11\pi }{5}.

Câu 8 (1đ):

Giá trị của các hàm số lượng giác $\sin \dfrac{5\pi }{4}$ ; $\sin \dfrac{5\pi }{3}$ lần lượt bằng

\dfrac{\sqrt{2}}{2}; \, \dfrac{-\sqrt{3}}{2}

.

\dfrac{-\sqrt{2}}{2}; \, \dfrac{\sqrt{3}}{2}

.

\dfrac{-\sqrt{2}}{2}; \, \dfrac{-\sqrt{3}}{2}

.

\dfrac{\sqrt{2}}{2}; \, \dfrac{\sqrt{3}}{2}

.

Câu 9 (1đ):

Tìm hiểu thời gian hoàn thành một bài kiểm tra đánh giá thường xuyên (đơn vị: phút) của một số học sinh thu được kết quả sau:

Thời gian (phút)	$\left[ 10;11 \right)$	$\left[ 11;12 \right)$	$\left[ 12;13 \right)$	$\left[ 13;14 \right)$	$\left[ 14;15 \right)$
Số học sinh	$1$	$2$	$5$	$12$	$20$

Thời gian trung bình (phút) để hoàn thành bài kiểm tra của các em học sinh là

10,5

.

14,5

.

13,7

.

12,3

.

Câu 10 (1đ):

Tổng $n$ số hạng đầu tiên của một cấp số cộng cho bởi $S_{n} = 3n^{2} - n$ . Công sai của cấp số cộng đó là

d = 6

.

d = 7

.

d = 5

.

d = 4

.

Câu 11 (1đ):

Cho phương trình $\cos \left(2x-\dfrac{\pi }{3} \right)-m=2$ . Giá trị của $m$ để phương trình có nghiệm là

m\in \left[ -3;-1 \right]

.

m\in \left[ -1;3 \right]

.

m\in \mathbb{R}

.

m \in \varnothing

.

Câu 12 (1đ):

Cho $\cot a=15$ , giá trị $\sin 2a$ bằng

\dfrac{17}{113}

.

\dfrac{15}{113}

.

\dfrac{13}{113}

.

\dfrac{11}{113}

.

Câu 13 (1đ):

Cho mẫu số liệu ghép nhóm về lương của nhân viên trong một công ty như sau:

Lương (triệu đồng)	$[9 ; 12)$	$[12 ; 15)$	$[15 ; 18)$	$[18 ; 21)$	$[21 ; 24)$
Số nhân viên	$6$	$12$	$4$	$2$	$1$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Giá trị đại diện của nhóm $\left[ 9;12 \right)$ là $10,5$ .
b) Trung bình lương các nhân viên là $16,5$ triệu đồng.
c) Nhóm chứa trung vị là $\left[ 15;18 \right)$ .
d) Tứ phân vị thứ ba là $15,56$ .

Câu 14 (1đ):

Bà Hoa gửi vào một ngân hàng số tiền $200$ triệu đồng với lãi suất $5\%$ một năm theo hình thức lãi kép, kì hạn $1$ tháng. Số tiền (triệu đồng) của bà Hoa sau $n$ tháng được tính theo công thức $T_n=200\Big(1+\dfrac{0,05}{12}\Big)^n$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Sau $1$ tháng, số tiền bà Hoa nhận được là khoảng $200,83$ (triệu đồng).
b) Sau $2$ tháng, số tiền bà nhận được là khoảng $201,67$ (triệu đồng).
c) Sau $14$ tháng, số tiền bà nhận được là khoảng $211,99$ (triệu đồng).
d) Sau $17$ tháng, số tiền bà nhận được là khoảng $215,65$ (triệu đồng).

Câu 15 (1đ):

Chiều cao so với mực nước biển trung bình tại thời điểm $t$ của mỗi cơn sóng được cho bởi hàm số $h(t)=75\sin \Big( \dfrac{\pi t}{8} \Big)$ , trong đó $h(t)$ được tính bằng centimét.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Chiều cao của sóng tại các thời điểm $5$ giây bằng $69,3$ cm.
b) Chiều cao của sóng tại các thời điểm $20$ giây bằng $75$ cm.
c) Trong $30$ giây đầu tiên, thời điểm để sóng đạt chiều cao lớn nhất là $6$ giây.
d) Trong $30$ giây đầu tiên, có $3$ thời điểm để sóng đạt chiều cao lớn nhất.

Câu 16 (1đ):

Để tích lũy cho việc học đại học của cậu con trai đầu lòng, cô Lan quyết định hằng tháng bỏ ra $600$ nghìn đồng vào tài khoản tiết kiệm, được trả lãi $0,5\%$ cộng dồn hằng tháng. Cô bắt đầu chương trình tích lũy này khi cậu con trai tròn ba tuổi và gửi tiền vào đầu mỗi tháng.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Đến lần gửi khoản tiền thứ $180$ thì cậu con trai tròn $18$ tuổi.
b) Số tiền của cô Lan có trong chương trình ở đầu tháng thứ $2$ là $0,6(1+0,5\%)$ triệu đồng.
c) Số tiền của cô Lan có trong chương trình ở đầu tháng thứ $5$ là $3 \, 030 \, 000$ đồng.
d) Số tiền của cô Lan có trong chương trình vào thời điểm cậu con trai đầu lòng tròn $18$ tuổi nhỏ hơn $160$ triệu đồng.

Câu 17 (1đ):

Nguời ta thiết kế một cái tháp gồm $10$ tầng theo cách: Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích bề mặt trên của tầng ngay bên dưới và diện tích bề mặt của tầng $1$ bằng nửa diện tích bề mặt đế tháp. Biết diện tích bề mặt đế tháp là $12 \, 288$ m $^2$ , tính diện tích bề mặt trên cùng của tháp (đơn vị mét vuông).

Trả lời:

Câu 18 (1đ):

Ông Sơn trồng cây trên một mảnh đất hình tam giác theo quy luật: ở hàng thứ nhất có $1$ cây, hàng thứ hai có $2$ cây, hàng thứ ba có $3$ cây…, ở hàng thứ $n$ có $n$ cây. Biết rằng ông đã trồng hết $11 \, 325$ cây. Số hàng cây được trồng theo cách trên là bao nhiêu?

Trả lời:

Câu 19 (1đ):

Trong môn cầu lông, khi phát cầu, người chơi cần đánh cầu qua khỏi lưới sang phía sân đối phương và không được để cho cầu rơi ngoài biên. Trong mặt phẳng toạ độ $Oxy$ , chọn điểm có tọa độ $\left(O;y_0\right)$ là điểm xuất phát thì phương trình quỹ đạo của cầu lông khi rời khỏi mặt vợt là: $y=\dfrac{-g.x^2}{2.v_{0}^{2}.\cos^{2}\alpha}+\tan (\alpha).x+y_0$ ; trong đó: $g$ là gia tốc trọng trường (thường được chọn là $9,8$ m/s $^{2}$ ; $\alpha$ là góc phát cầu (so với phương ngang của mặt đất); ${{v}_{0}}$ là vận tốc ban đầu của cầu; ${{y}_{0}}$ là khoảng cách từ vị trí phát cầu đến mặt đất. Quỹ đạo chuyển động của quả cầu lông là một parabol như hình vẽ.

loading...

Một người chơi cầu lông đang đứng khoảng cách từ vị trí người này đến vị trí cầu rơi chạm đất (tầm bay xa) là $6,68$ m. Người chơi đó đã phát cầu với góc tối đa khoảng bao nhiêu độ so với mặt đất? (biết cầu rời mặt vợt ở độ cao $0,7$ m so với mặt đất và vận tốc xuất phát của cầu là $8$ m/s, bỏ qua sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng thẳng đứng, làm tròn kết quả tới hàng đơn vị).

Trả lời:

Câu 20 (1đ):

Trên nóc một tòa nhà có một cột ăng-ten cao $5$ m. Từ vị trí quan sát $A$ cao $7$ m so với mặt đất, có thể nhìn thấy đỉnh $B$ và chân $C$ của cột ăng-ten dưới góc $\alpha$ và $\beta$ so với phương nằm ngang.

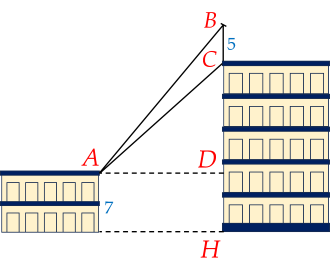
loading...

Biết chiều cao của toà nhà là $18,9$ m, hai toà nhà cách nhau $10$ m. Tính góc $\alpha = \widehat{BAD}$ (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).

Trả lời:

Câu 21 (1đ):

Cho cấp số nhân $(v_n)$ . Biết rằng ba số $v_1, \, v_4$ và $v_7$ lần lượt là các số hạng thứ nhất, thứ hai và thứ mười của một cấp số cộng có công sai $d \ne 0$ . Tìm công bội $q$ của cấp số nhân $(v_n)$ .

Trả lời:

Câu 22 (1đ):

Cho hình vuông $(C_1)$ có cạnh bằng $a$ . Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông $(C_2)$ .

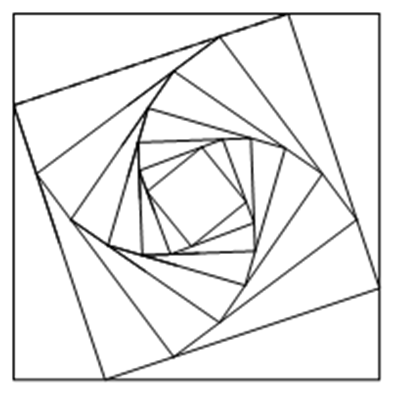
Từ hình vuông $(C_2)$ lại tiếp tục làm như trên ta nhận được dãy các hình vuông $C_1$ , $C_2$ , $C_3$ ,..., $C_n$ . Gọi $S_i$ là diện tích của hình vuông $C_i, \, (i \in \left\{ 1;2;3,..... \right\})$ . Đặt $T=S_1+S_2+S_3+...+S_n+...$ . Biết $T=\dfrac{32}{3}$ , tính $a$ ?

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP