Đề kiểm tra học kì I (đề số 3)

Câu 1 (1đ):

Cho $2\pi \lt \alpha \lt \dfrac{5\pi }{2}$ , kết quả nào sau đây đúng?

\tan \alpha \lt 0;\cot \alpha >0

.

\tan \alpha \lt 0;\cot \alpha \lt 0

.

\tan \alpha >0;\cot \alpha >0

.

\tan \alpha >0;\cot \alpha \lt 0

.

Câu 2 (1đ):

Nghiệm của phương trình $\sin x=1$ là

x=\dfrac{\pi }{2}+k2\pi

,

k\in \mathbb{Z}

.

x=-\dfrac{\pi }{2}+k2\pi

,

k\in \mathbb{Z}

.

x=\dfrac{\pi }{2}+k\pi

,

k\in \mathbb{Z}

.

x=k\pi

,

k\in \mathbb{Z}

.

Câu 3 (1đ):

Dãy số nào sau đây không phải cấp số cộng?

-8; \, -6; \, -4; \, -2;\, 0

.

\dfrac{1}{2}; \, \dfrac{3}{2}; \, \dfrac{5}{2}; \, \dfrac{7}{2}; \, \dfrac{9}{2}

.

1;\,1;\,1;\,1;\,1

.

3; \, 1; \, -1; \, -2; \, -4

.

Câu 4 (1đ):

Cho dãy số $(u_n)$ biết $\left\{ \begin{aligned}&u_1=3 \\&u_{n+1}=3u_n\\ \end{aligned}\right., \, \forall n \in \mathbb{N}^*$ . Số hạng tổng quát của dãy số $(u_n)$ là

u_n=3^{n+1}

.

u_n=n^{n+1}

.

u_n=3^{n-1}

.

u_n=3^n

.

Câu 5 (1đ):

$\underset{x \to -1}{\mathop{\lim}}\dfrac{2x^3+x^2+4}{2x^5+3}$ bằng

1

.

\dfrac75

.

7

.

3

.

Câu 6 (1đ):

$\underset{x \to 3^-}{\mathop{\lim}} \dfrac{1}{x-3}$ bằng

-\infty

.

-\dfrac16

.

0

.

+\infty

.

Câu 7 (1đ):

Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Thời gian (phút)	Số học sinh
$\big[0 \, ; \, 20\big)$	$5$
$\big[20 \, ; \, 40\big)$	$9$
$\big[40 \, ; \, 60\big)$	$12$
$\big[60 \, ; \, 80\big)$	$10$
$\big[80 \, ; \, 100\big)$	$6$

Nhóm chứa mốt của mẫu số liệu trên là

\big[80;100\big)

.

\big[60;80\big)

.

\big[40;60\big)

.

\big[20;40\big)

.

Câu 8 (1đ):

Cho mặt phẳng $(P)$ và điểm $M$ không nằm trong mặt phẳng $(P)$ . Có bao nhiêu mặt phẳng đi qua điểm $M$ và song song với mặt phẳng $(P)$ ?

1

.

0

.

Vô số.

2

.

Câu 9 (1đ):

Hai đường thẳng $a$ và $b$ nằm trong $(\alpha)$ . Hai đường thẳng $a'$ và $b'$ nằm trong mặt phẳng $(\beta)$ . Mệnh đề nào sau đây đúng?

A

Nếu

a

//

a'

và

b

//

b'

thì

(\alpha)

//

(\beta)

.

B

Nếu

a

cắt

b

,

a'

cắt

b'

và

a

//

a'

và

b

//

b'

thì

(\alpha)

//

(\beta)

.

C

Nếu

(\alpha)

//

(\beta)

thì

a

//

a'

và

b

//

b'

.

D

Nếu

a

//

b

và

a'

//

b'

thì

(\alpha)

//

(\beta)

.

Câu 10 (1đ):

Cho hình bình hành $ABCD$ và $S$ là điểm không thuộc mặt phẳng của hình bình hành. Giao tuyến của $(SAD)$ và $(SBC )$ là

SI

với

I

là giao điểm của

AD

và

BC

.

SO

với

O

là giao điểm của

AC

và

BD

.

Đường thẳng qua

S

và song song với

AB

.

Đường thẳng qua

S

và song song với

AD

.

Câu 11 (1đ):

Giới hạn $L=\lim (\sqrt{4n^2+n}-\sqrt{4n^2+2})$ bằng

-7

.

\dfrac{1}{4}

.

-\infty

.

+\infty

.

Câu 12 (1đ):

Giới hạn $\underset{x \to +\infty }{\mathop{\lim}} \dfrac{\sqrt{x^2+2}-2}{x-2}$ bằng

1

.

-1

.

+\infty

.

-\infty

.

Câu 13 (1đ):

Một bảng giá cước taxi được cho như sau:

Giá mở cửa

( $0,5$ km)

Giá cước các km tiếp theo đến $30$ km

Giá cước từ km thứ $31$

$10 \, 000$ đồng

$13\,500$ đồng

$11\,000$ đồng

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Khi $x>30$ , tiền cước là $f(x)=11\,000(x-30)$ .
b) Công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển $f(x)=\left\{ \begin{aligned} & 10\,000x\,\, khi \,\,x\le 0,5 \\ & 5\,000+13\,500(x-0,5)\,\, khi \,\,0,5\lt x\le 30 \\ & 403\,250+11\,000(x-30)\,\, khi \,\,x>30 \\ \end{aligned} \right.$ .
c) Hàm số $f(x)=\left\{ \begin{aligned} & 10\,000x\,\, khi \,\,x\le 0,5 \\ & 5\,000+13\,500(x-0,5)\,\, khi \,\,0,5\lt x\le 30 \\ & 403 \, 250+11\,000(x-30)\,\, khi \,\,x>30 \\ \end{aligned} \right.$ liên tục trên $\mathbb{R}$ .
d) Khách hàng đi quãng đường $40$ km thì số tiền vị khách đó phải trả là $515\,000$ đồng.

Câu 14 (1đ):

Cho hình chóp $S.ABC$ , gọi $G, \, H$ lần lượt là trọng tâm các tam giác $\Delta ABC$ và $\Delta SAB$ , $M$ là trung điểm của $AB.$ Lấy $P$ là một điểm nằm trên cạnh $BC$ khác $B$ và $C$ . Gọi $Q$ là giao điểm của $(PHG)$ và $SB$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $CG\cap (SAB)=M$ với $M$ là trung điểm của $SB$ .
b) $GH$ // $(SAC)$ .
c) Gọi $I$ là trọng tâm tam giác $SAC$ . Khi đó $SB$ // $(HGI)$ .
d) Tứ giác $HGPQ$ là hình bình hành khi $\dfrac{PC}{PB}=3$ .

Câu 15 (1đ):

Anh Bình là nhân viên của một công ty A. Từ ngày 1/2/2024 anh Bình được nâng lương lên bậc 4, mức lương anh hiện hưởng là $11$ $718$ $750$ đồng mỗi tháng. Theo quy định của công ty, nếu không bị kỉ luật, không có khen thưởng đặc biệt thì cứ sau $3$ năm anh Bình sẽ được nâng một bậc lương, tăng thêm $25\%$ so với bậc lương trước, tối đa là bậc 7. Khi hết bậc 7 sẽ chuyển sang vượt khung. Lương vượt khung năm sau cao hơn năm trước $1\%$ và vẫn nhận hàng tháng. Lương bậc 1 sẽ được tính sau khi hết đúng $1$ năm tập sự. Anh Bình là người rất nghiêm túc, không vi phạm kỉ luật. Anh dự định sẽ làm việc $30$ năm ở công ty này rồi nghỉ hưu.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Lương bậc 5 của anh Bình sẽ là $14$ $500$ $000$ đồng.
b) Lương bậc 1 của anh Bình là $6$ $000$ $000$ đồng.
c) Lương bậc 7 anh Bình là $23$ $250$ $000$ .
d) Tổng tiền lương anh Bình nhận được kể từ khi hết tập sự đến khi nghỉ hưu là $5 \, 554 \, 357 \, 709$ .

Câu 16 (1đ):

Dưới đây là 2 bảng thống kê doanh số bán hàng của 20 nhân viên tại một cửa hàng điện thoại trong tháng 9 đối với hai nhãn hàng Oppo và Samsung.

Bảng thống kê doanh số điện thoại bán được của Oppo trong tháng 9.

Doanh số	Số nhân viên
$\big[18 \, ; \, 20\big]$	$2$
$\big[21 \, ; \, 23\big]$	$5$
$\big[24 \, ; \, 26\big]$	$8$
$\big[27 \, ; \, 29\big]$	$3$
$\big[30 \, ; \, 32\big]$	$2$

Bảng thống kê doanh số điện thoại bán được của Samsung trong tháng 9.

Doanh số	Số nhân viên
$\big[15 \, ; \, 19\big]$	$5$
$\big[20 \, ; \, 24\big]$	$8$
$\big[25 \, ; \, 29\big]$	$5$
$\big[30 \, ; \, 34\big]$	$1$
$\big[35 \, ; \, 39\big]$	$1$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Đối với $20$ nhân viên bán hàng được khảo sát thì bảng thống kê cho thấy điện thoại của nhãn hàng Oppo dễ bán hơn so với điện thoại của hãng Samsung. (so sánh dựa trên giá trị trung bình của 2 bảng thống kê)
b) Đối với điện thoại của hãng Samsung, khả năng một nhân viên bán được $26$ chiếc là cao nhất. Chủ cửa hàng điện thoại muốn dành phần thưởng khích lệ cho các nhân viên bán được doanh số cao. Điều kiện được nhận quà là phải nằm trong Top 5 nhân viên đạt doanh số điện thoại Samsung cao nhất và đồng thời phải nằm trong Top 10 nhân viên đạt doanh số điện thoại Oppo cao nhất.
c) Anh An nghĩ mình sẽ nhận được thưởng vì anh An bán được $25$ chiếc điện thoại Oppo và $26$ chiếc điện thoại Samsung.
d) Chị Bình nghĩ mình cũng sẽ nhận được thưởng dù chị chỉ bán được $24$ chiếc điện thoại Oppo nhưng chị bán được tới $27$ chiếc điện thoại Samsung.

Câu 17 (1đ):

Thời gian (phút) di chuyển đến trường của nhóm học sinh trường THPT $A$ được tổng hợp dưới bảng sau:

Thời gian (phút)	Số học sinh
$\big[15 \, ; \, 20\big)$	$6$
$\big[20 \, ; \, 25\big)$	$14$
$\big[25 \, ; \, 30\big)$	$25$
$\big[30 \, ; \, 35\big)$	$37$
$\big[35 \, ; \, 40\big)$	$13$
$\big[40 \, ; \, 45\big)$	$9$
$\big[45 \, ; \, 50\big)$	$21$

Tìm trung vị của mẫu số liệu ghép nhóm trên? (làm tròn đến hàng phần mười)

Trả lời:

Câu 18 (1đ):

Vào đầu mỗi tháng, ông An đều gửi vào ngân hàng số tiền cố định $30$ triệu đồng theo hình thức lãi kép với lãi suất $0,6\%$ /tháng. Tính số tiền (đơn vị triệu đồng) ông An có được sau tháng sau tháng thứ hai. (làm tròn kết quả tới hàng phần mười)

Trả lời:

Câu 19 (1đ):

Chi phí (đơn vị: nghìn đồng) để sản xuất $x$ sản phẩm của một công ty được xác định bởi hàm số: $C(x)=15 \, 000+200x$ . Khi số sản phẩm sản xuất ra ngày càng nhiều thì chi phí trung bình chỉ tối đa là bao nhiêu nghìn đồng?

Trả lời:

Câu 20 (1đ):

Tìm tất cả các giá trị nguyên của tham số $m$ trong $[ -2;9 ]$ sao cho phương trình $(m^2-5m+4)x^5+x^2+4=0$ có nghiệm.

Trả lời:

Câu 21 (1đ):

Cho hàm số $y=f(x)=\left\{ \begin{aligned} & \dfrac{| 2x^2-7x+6 |}{x-2}\,\,khi\,\,x\lt 2 \\ & a+\dfrac{1-x}{2+x}\,\,khi\,\,x\ge 2 \\ \end{aligned} \right.$ . Biết $a$ là giá trị để hàm số $y = f(x)$ liên tục tại $x_0=2$ , bất phương trình $-x^2+ax+\dfrac74>0$ có bao nhiêu nghiệm nguyên?

Trả lời:

Câu 22 (1đ):

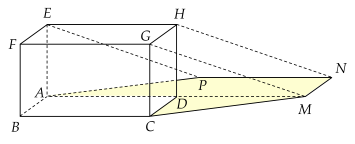
Vào một thời điểm trong ngày, người ta quan sát thấy bóng râm của một thùng hàng dạng hình hộp chữ nhật $ABCD.EFGH$ là hình chiếu của thùng hàng đó lên mặt đất với phương chiếu $GM$ song song với các tia sáng mặt trời (các tia sáng mặt trời được xem là các đường thẳng song song với nhau), $M$ trùng với điểm đối xứng với $A$ qua $D$ . Tính diện tích phần bóng râm được tô màu trong hình vẽ bên dưới, biết rằng $BC=8$ m, $CD=2$ m và $CG=4$ m. (kết quả tính theo đơn vị m $^2$ )

Vào một thời điểm trong ngày, người ta quan sát thấy bóng râm của một thùng hàng dạng hình hộp chữ nhật

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP