\(ℕ,ℤ,ℚ,ℝ,C\) lần lượt là tập hợp các số tự nhiên, số nguyên, số hữu tỉ, số thực và số phức.

 Do đó \(ℕ\subsetℤ\subsetℚ\subsetℝ\subset C\)

 Nếu cái bạn đang nói đến là tích phân thì \(f\left(x\right)|^a_b=f\left(a\right)-f\left(b\right)\). 

 Ví dụ: Tính tích phân \(I=\int\limits^1_02xdx\)

 Giải: \(I=\int\limits^1_02xdx=x^2|^1_0=1^2-0^2=1\)

a) A chia hết cho 3 nhưng không chia hết cho 9 \(\Rightarrow\) A không là số chính phương.

b) \(100!⋮4\) và 7 chia 4 dư 3 nên \(100!+7\) chia 4 dư 3. Do đó nó cũng không phải là SCP.

c) B chia hết cho 11 nhưng không chia hết cho 11² nên B không là SCP.

Điều kiện: \(x\ge2;y\ge-2024;z\ge2025\)

Ta có \(\sqrt{x-2}=\sqrt{1.\left(x-2\right)}\le\dfrac{1+x-2}{2}=\dfrac{x-1}{2}\) (bđt Cô-si)

\(\sqrt{y+2024}=\sqrt{1.\left(y+2024\right)}\le\dfrac{1+y+2024}{2}=\dfrac{y+2025}{2}\)

\(\sqrt{z-2025}=\sqrt{1.\left(z-2025\right)}\le\dfrac{1+z-2025}{2}=\dfrac{z-2024}{2}\)

Cộng theo vế 3 bđt trên, ta có:

\(VP=\sqrt{x-2}+\sqrt{y+2024}+\sqrt{z-2025}\)

\(\le\dfrac{x-1}{2}+\dfrac{y+2025}{2}+\dfrac{z-2024}{2}\)

\(=\dfrac{1}{2}\left(x+y+z\right)=VP\)

Như vậy dấu "=" phải xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x-2=1\\y+2024=1\\z-2025=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-2023\\z=2026\end{matrix}\right.\) (nhận)

Vậy pt đã cho có nghiệm \(\left(x,y,z\right)=\left(3,-2023,2026\right)\)

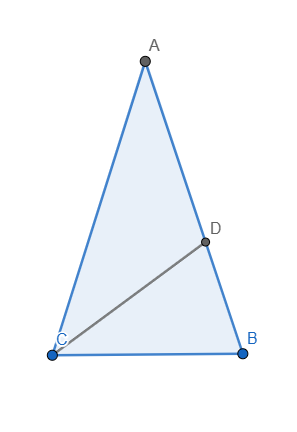
hình bài 2

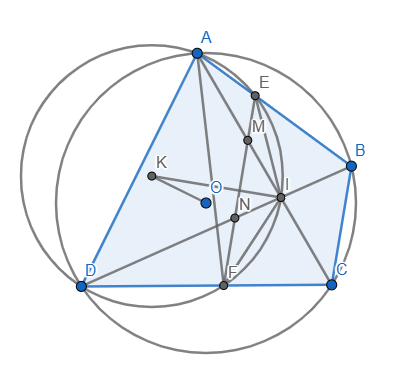
hình bài 1

1)

a) Tứ giác ABCD nội tiếp \(\Rightarrow\widehat{ABC}=180^o-\widehat{ADC}\)

Tứ giác AEFD nội tiếp \(\Rightarrow\widehat{AEF}=180^o-\widehat{ADF}=180^o-\widehat{ADC}\)

\(\Rightarrow\widehat{ABC}=\widehat{AEF}\)

\(\Rightarrow\) EF//BC (2 góc đồng vị bằng nhau)

\(\Rightarrow\widehat{IMN}=\widehat{ICB}\) (2 góc so le trong)

Mà \(\widehat{ICB}=\widehat{ACB}=\widehat{ADB}=\widehat{ADN}\) nên \(\widehat{IMN}=\widehat{ADN}\)

\(\Rightarrow\) Tứ giác AMND nội tiếp (góc ngoài bằng góc trong đối) (đpcm)

b) Tứ giác ABCD nội tiếp \(\Rightarrow\widehat{BAC}=\widehat{BDC}\) hay \(\widehat{EAI}=\widehat{FDI}\)

Lại có \(\widehat{EAI}\) và \(\widehat{FDI}\) là các góc nội tiếp chắn các cung EI, FI của đường tròn (K)

\(\Rightarrow\stackrel\frown{EI}=\stackrel\frown{FI}\Rightarrow EI=FI\)

\(\Rightarrow\) I thuộc trung trực của đoạn EF.

Mà \(KE=KF\Rightarrow\) K cũng thuộc trung trực của đoạn EF

\(\Rightarrow\) IK là trung trực EF \(\Rightarrow IK\perp EF\)

Mà EF//BC (cmt) \(\Rightarrow IK\perp BC\) (đpcm)

2) 

Trên cạnh BC lấy điểm D sao cho tam giác BCD cân tại B. Dễ thấy \(\Delta CBD\sim\Delta CAB\)

\(\Rightarrow\widehat{CBD}=\widehat{BAC}=\widehat{DAB}=36^o\)

\(\Rightarrow\widehat{DBA}=\widehat{CBA}-\widehat{DBC}=72^o-36^o=36^o\)

\(\Rightarrow\widehat{DAB}=\widehat{DBA}\)

\(\Rightarrow\Delta DAB\) cân tại D \(\Rightarrow DA=DB\)

Đặt \(DA=DB=BC=a\), \(CD=b\) \(\left(a>b\right)\)

Khi đó vì \(\Delta CBD\sim\Delta CAB\) nên \(\dfrac{a+b}{a}=\dfrac{a}{b}\) 

\(\Leftrightarrow ab+b^2=a^2\) 

\(\Leftrightarrow-a^2+ab+b^2=0\)

\(\Leftrightarrow-\left(\dfrac{a}{b}\right)^2+\dfrac{a}{b}+1=0\)

\(\Leftrightarrow\dfrac{a}{b}=\dfrac{1+\sqrt{5}}{2}\) (loại nghiệm \(\dfrac{a}{b}=\dfrac{1-\sqrt{5}}{2}\) vì \(\dfrac{a}{b}>1\))

hay \(\dfrac{a+b}{a}=\dfrac{1+\sqrt{5}}{2}\) hay \(\dfrac{AB}{BC}=\dfrac{1+\sqrt{5}}{2}\)

\(N=\dfrac{x^2+x+1}{x^2+1}\)

\(\Leftrightarrow\left(x^2+1\right)N=x^2+x+1\)

\(\Leftrightarrow Nx^2+N=x^2+x+1\)

\(\Leftrightarrow\left(N-1\right)x^2-x+N-1=0\) (*)

Có \(\Delta=\left(-1\right)^2-4\left(N-1\right)^2\) 

\(=1-\left(2N-2\right)^2\)

\(=\left(1+2N-2\right)\left(1-2N+2\right)\)

\(=\left(2N-1\right)\left(3-2N\right)\)

Để (*) có nghiệm thì \(\Delta=\left(2N-1\right)\left(3-2N\right)\ge0\)

\(\Leftrightarrow\dfrac{1}{2}\le N\le\dfrac{3}{2}\)

\(N=\dfrac{1}{2}\) khi \(x=-\dfrac{-1}{2\left(N-1\right)}=\dfrac{1}{2\left(\dfrac{1}{2}-1\right)}=-1\)

\(N=\dfrac{3}{2}\) khi \(x=-\dfrac{-1}{2\left(N-1\right)}=\dfrac{1}{2\left(\dfrac{3}{2}-1\right)}=1\)

Vậy \(minN=\dfrac{1}{2}\) khi \(x=-1\) và \(maxN=\dfrac{3}{2}\) khi \(x=1\)

\(Q=mc\Delta t=5.3870.\left(50-20\right)=580500\left(J\right)\)

 Có tất cả \(A^2_{30}=870\) véc-tơ thỏa mãn yêu cầu bài toán (chọn ra 2 đỉnh trong 30 đỉnh sau đó chọn ra 1 điểm gốc và 1 điểm cuối)