Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra học kì I (đề số 2) SVIP
Tải đề xuống bằng file Word
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho cấp số cộng (un) với u1=1 và u100=496. Công sai của cấp số cộng đã cho bằng
Cho dãy số có các số hạng đầu là 31;321;331;341;.... Số hạng tổng quát của dãy số này là
limn2018 bằng
Cho hàm số y=f(x) có đồ thị như hình vẽ:
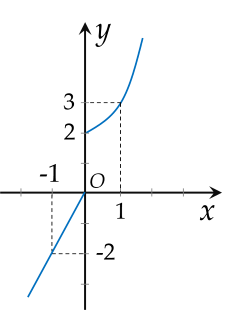
Hàm số không liên tục tại điểm
Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
| Thời gian (phút) | Số học sinh |
| [0;20) | 5 |
| [20;40) | 9 |
| [40;60) | 12 |
| [60;80) | 10 |
| [80;100) | 6 |
Nhóm chứa mốt của mẫu số liệu trên là
Cho phép chiếu song song, biết rằng các đường thẳng dưới đây có phương không trùng với phương chiếu. Khẳng định nào sau đây đúng?
Khẳng định nào sau đây sai?
Quan sát các vạch chỉ đường cho người đi bộ sang đường:

Vị trí tương đối của các vạch đó là
Tất cả các giá trị của m để phương trình sinx=2m có hai nghiệm phân biệt trên đoạn [0;π] là
Cho dãy số (un) với un=2n−1. Khi đó, (un) là dãy số
Có bao nhiêu dãy số là cấp số cộng trong năm dãy số cho sau đây?
(1) Dãy (un) xác định bởi un=n2 với mọi số nguyên dương n.
(2) Dãy (un) xác định bởi un=(−1)n.n với mọi số nguyên dương n.
(3) Dãy (un) xác định bởi un=2(n+3)−5 với mọi số nguyên dương n.
(4) Dãy (un) xác định bởi u0=a,u1=b,un+1=2un+un−1 trong đó hằng số a,b khác nhau cho trước, với mọi số nguyên dương n.
(5) Dãy (un) xác định bởi u0=2022, u1=2021, un+1=2un−un−1 với mọi số nguyên dương n.
x→−∞lim(x2+x+2x) bằng
Một bãi đậu xe ô tô đưa ra giá T(x) (đồng) khi thời gian đậu xe là x (giờ) như sau: T(x)=⎩⎨⎧50000khi0<x≤2120000khi2<x<435000xkhix≥4
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) T(2)=50000. |
|
| b) x→4+limT(x)=120000. |
|
| c) Hàm số T(x) liên tục tại x=4. |
|
| d) Hàm số T(x) liên tục trên [4;+∞). |
|
Khảo sát chiều cao của học sinh lớp 11C1, thu được bảng số liệu ghép nhóm như sau
| Khoảng chiều cao (cm) | Số học sinh |
| [150;155) | 7 |
| [155;160) | 15 |
| [160;165) | 12 |
| [165;170) | 8 |
| [170;175) | 3 |
| a) Lớp 11C1 có 43 học sinh. |
|
| b) Chiều cao trung bình của học sinh 11C1 thuộc khoảng (161;162). |
|
| c) Số học sinh có chiều cao không dưới 160 cm là 22 học sinh. |
|
| d) Trung vị của mẫu số liệu ghép nhóm trên là 6961 cm. |
|
Cho hình chóp S.ABCD có đáy là hình thang AB // CD,AB=2CD, M là trung điểm cạnh AB.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) MC // (SAD). |
|
| b) Giao tuyến của hai mặt phẳng (SAD) và (SMC) là đường thẳng Sx với Sx // AD. |
|
| c) AM=DC. |
|
| d) (P) là mặt phẳng qua M và song song với hai đường thẳng SB,SD. Gọi E là giao điểm của CD với (P), khi đó DCEC=21. |
|
Để tích lũy cho việc học đại học của cậu con trai đầu lòng, cô Lan quyết định hằng tháng bỏ ra 600 nghìn đồng vào tài khoản tiết kiệm, được trả lãi 0,5% cộng dồn hằng tháng. Cô bắt đầu chương trình tích lũy này khi cậu con trai tròn ba tuổi và gửi tiền vào đầu mỗi tháng.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Đến lần gửi khoản tiền thứ 180 thì cậu con trai tròn 18 tuổi. |
|
| b) Số tiền của cô Lan có trong chương trình ở đầu tháng thứ 2 là 0,6(1+0,5%) triệu đồng. |
|
| c) Số tiền của cô Lan có trong chương trình ở đầu tháng thứ 5 là 3030000 đồng. |
|
| d) Số tiền của cô Lan có trong chương trình vào thời điểm cậu con trai đầu lòng tròn 18 tuổi nhỏ hơn 160 triệu đồng. |
|
Chiều cao (đơn vị: m) của 35 cây bạch đàn được cho ở bảng sau:
Số đo chiều cao (m)
|
Số cây |
[6,5;7) | 6 |
[7;7,5) | 9 |
[7,5;8) | 15 |
[8;8,5) | 4 |
[8,5;9) | 1 |
Trung vị của mẫu số liệu ghép nhóm trên bằng bao nhiêu? (Làm tròn kết quả đến hàng phần trăm)
Trả lời:
Ông Sơn trồng cây trên một mảnh đất hình tam giác theo quy luật: ở hàng thứ nhất có 1 cây, hàng thứ hai có 2 cây, hàng thứ ba có 3 cây…, ở hàng thứ n có n cây. Biết rằng ông đã trồng hết 11325 cây. Số hàng cây được trồng theo cách trên là bao nhiêu?
Trả lời:
Biết rằng x→+∞limx−x2+1(2−a)x−3=+∞ (với a là tham số). Giá trị nhỏ nhất của P=a2−2a+4 bằng bao nhiêu?
Trả lời:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, ABC=60∘, AB=8. Gọi O,M lần lượt là trung điểm của BC,AB. Mặt phẳng (α) qua M và song song với SB và OA, cắt BC,SC,SA lần lượt tại N,P,Q. Tính diện tích của tứ giác MNPQ, biết SB⊥OA và SB=8.
Trả lời:
Vào một thời điểm trong ngày, người ta quan sát thấy bóng râm của một thùng hàng dạng hình hộp chữ nhật ABCD.EFGH là hình chiếu của thùng hàng đó lên mặt đất với phương chiếu GM song song với các tia sáng mặt trời (các tia sáng mặt trời được xem là các đường thẳng song song với nhau), M trùng với điểm đối xứng với A qua D. Tính diện tích phần bóng râm được tô màu trong hình vẽ bên dưới, biết rằng BC=8 m, CD=2 m và CG=4 m. (kết quả tính theo đơn vị m2)
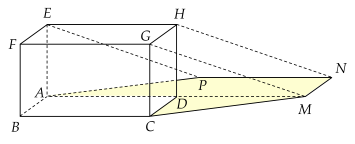
Trả lời:
