Đề kiểm tra số 1

Câu 1 (1đ):

Cho $A=\left[-1;5 \right), \, B=\left(2;7 \right]$ . Tập $A \backslash B$ là

\left[-1;2 \right)

.

\left(2;5 \right)

.

\left[-1;2 \right]

.

\left[-1;7 \right]

.

Câu 2 (1đ):

Cặp số nào sau đây là nghiệm của bất phương trình $2x-3y \le 6$ ?

(2 ; -3)

.

(4 ; -1)

.

(-2 ; -5)

.

(2 ; 1)

.

Câu 3 (1đ):

Trên nửa đường tròn đơn vị, cho góc $\alpha$ như hình vẽ:

loading...

Các giá trị lượng giác của góc $\alpha$ là

\sin \alpha =1

;

\cos \alpha =0

;

\tan \alpha =0

;

\cot \alpha

không xác định.

\sin \alpha =0

;

\cos \alpha =1

;

\tan \alpha =1

;

\cot \alpha =0

.

\sin \alpha =1

;

\cos \alpha =0

;

\tan \alpha

không xác định;

\cot \alpha =0

.

\sin \alpha =1

;

\cos \alpha =0

;

\tan \alpha

không xác định;

\cot \alpha =1

.

Câu 4 (1đ):

Cho tam giác $ABC$ vuông tại $A$ , $G$ là trọng tâm tam giác $ABC,\, BC=a$ . Độ dài vectơ $\overrightarrow{AG}$ là

\dfrac{a}{6}

.

\dfrac{a}{3}

.

\dfrac{a\sqrt{3}}2

.

\dfrac{2a}{3}

.

Câu 5 (1đ):

Từ hai điểm phân biệt $A,\, B$ xác định được bao nhiêu vectơ khác $\overrightarrow{0}$ ?

2.

3.

1.

4.

Câu 6 (1đ):

Câu 7 (1đ):

Câu 8 (1đ):

Tam giác $ABC$ có $\widehat{A}=105^\circ$ , $\widehat{B}=45^\circ$ , $AC=10$ . Độ dài cạnh $AB$ bằng

5\sqrt{2}

.

10\sqrt{2}

.

\dfrac{5\sqrt{6}}{2}

.

5\sqrt{6}

.

Câu 9 (1đ):

Mệnh đề phủ định của mệnh đề $P$ : " $\sqrt{2} \le 2$ " là

\overline{P}:

"

\sqrt{2} \ne 2

".

\overline{P}:

"

\sqrt{2}>2

".

\overline{P}:

"

\sqrt{2}\ge 2

".

\overline{P}:

"

\sqrt{2}<2

".

Câu 10 (1đ):

Cho tam giác $ABC$ đều cạnh $a$ . Độ dài vectơ $\overrightarrow{AB}+\overrightarrow{AC}$ là

2a

.

a\sqrt{3}

.

2a\sqrt{3}

.

\dfrac{a\sqrt{3}}2

.

Câu 11 (1đ):

Cho tam giác $ABC$ . Gọi $I$ là trung điểm của $AB$ . Điểm $M$ thỏa mãn hệ thức $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}$ là

điểm trên cạnh

IC

sao cho

IM=2MC

.

trung điểm của

IC

.

trung điểm của

BC

.

trung điểm của

IA

.

Câu 12 (1đ):

Cho hai vectơ $\overrightarrow{a}$ ; $\overrightarrow{b}$ khác vectơ $\overrightarrow{0}$ thỏa mãn $\overrightarrow{a}.\overrightarrow{b}=\dfrac12\left| -\overrightarrow{a} \right|.\left| \overrightarrow{b} \right|$ . Khi đó góc giữa hai vectơ $\overrightarrow{a}$ ; $\overrightarrow{b}$ bằng

150^\circ

.

120^\circ

.

60^\circ

.

30^\circ

.

Câu 13 (1đ):

Bác Minh có kế hoạch đầu tư không quá $240$ triệu đồng vào hai khoản $X$ và khoản $Y$ . Để đạt được lợi nhuận thì khoản $Y$ phải đầu tư ít nhất $40$ triệu đồng và số tiền đầu tư cho khoản $X$ phải ít nhất gấp ba lần số tiền cho khoản $Y$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Gọi $x, \, y$ (đơn vị: triệu đồng) lần lượt là số tiền bác Minh đầu tư vào khoản $X$ và khoản $Y$ , ta có hệ bất phương trình: $\left\{ \begin{aligned} &x+y \le 240 \\&y \ge 40 \\&x \ge 3y \\ \end{aligned} \right.$ .
b) Điểm $C(200;40)$ không thuộc miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư.
c) Điểm $A(180;60)$ là điểm có tung độ lớn nhất thuộc miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư.
d) Miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư là một tứ giác.

Câu 14 (1đ):

Cho tam giác $ABC$ biết $a=8$ dm, $\widehat{B}=45^\circ, \, \widehat{C}=60^\circ$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\widehat{A}=75^\circ$ .
b) $\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$ .
c) $b \approx 5,26$ cm.
d) $c \approx 3,17$ cm.

Câu 15 (1đ):

Cho tam giác $ABC$ có trực tâm $H$ và $M$ là trung điểm $BC$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{HA}.\overrightarrow{CB}=1$ .
b) $\overrightarrow{BH}.\overrightarrow{CA}=0$ .
c) $\overrightarrow{MH}.\overrightarrow{MA}=\dfrac{BC^2}{4}$ .
d) $MH^2+MA^2=AH^2+\dfrac{BC^2}{2}$ .

Câu 16 (1đ):

Cuối học kì I vừa qua, bạn An đạt được kết quả sáu môn như sau:

Môn	Điểm trung bình
Toán	$7,2$
Văn	$8,0$
Anh	$5,8$
Lý	$7,2$
Hóa	$9,0$
Sinh	$4,6$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Điểm trung bình các môn thi học kì của bạn An là $7,0$ .
b) Điểm trung bình các môn thi học kì của bạn An là $7,3$ .
c) Khoảng biến thiên của bảng điểm của bạn An bằng $3,4$ .
d) Khoảng tứ phân vị bảng điểm của bạn An bằng $2,2$ .

Câu 17 (1đ):

Cho hình thoi $ABCD$ có $\widehat{BAD}=60^\circ$ và $BD=a$ . Gọi $M, \, N$ lần lượt là trung điểm của $AD, \, DC$ . Tích $\overrightarrow{BM}.\overrightarrow{BN}$ bằng $\dfrac{ma^2}n$ với $\dfrac mn$ là phân số tối giản có mẫu dương. Tính $m + n$ .

Trả lời:

Câu 18 (1đ):

Hai bạn An và Bình cùng di chuyển một xe đẩy trên đường phẳng bằng cách: bạn An đẩy xe từ phía sau theo hướng di chuyển của xe bằng một lực $F_1=2$ N, bạn Bình kéo xe từ phía trước theo hướng di chuyển của xe một lực $F_2=3$ N. Giả sử hai bạn thực hiện đúng kỹ thuật để xe di chuyển hiệu quả nhất. Xe di chuyển với lực tác động có độ lớn bằng bao nhiêu N?

Trả lời:

Câu 19 (1đ):

Để được cấp chứng chỉ môn Anh trình độ A2 của một trung tâm ngoại ngữ, học viên phải trải qua $6$ lần kiểm tra trắc nghiệm, thang điểm mỗi lần kiểm tra là $100$ và phải đạt điểm trung bình từ $70$ điểm trở lên. Qua $5$ lần thi Hoa đạt điểm trung bình là $64,5$ điểm. Trong lần kiểm tra cuối cùng Hoa phải đạt ít nhất là bao nhiêu điểm để được cấp chứng chỉ?

Trả lời:

Câu 20 (1đ):

Một người thợ mộc làm hai loại sản phẩm là bàn và ghế. Mỗi cái bàn khi bán lãi $150$ nghìn đồng, mỗi cái ghế khi bán lãi $50$ nghìn đồng. Người thợ mộc có thể làm $40$ giờ/tuần và tốn $6$ giờ để làm một cái bàn, $3$ giờ để làm một cái ghế. Khách hàng yêu cầu người thợ mộc làm số ghế ít nhất là gấp ba lần số bàn. Một cái bàn chiếm chỗ bằng $4$ cái ghế và ta có phòng để được nhiều nhất $4$ cái bàn. Người thợ mộc phải sản xuất $x$ cái bàn và $y$ cái ghế trong ba tuần để số tiền lãi thu về là lớn nhất. Tính $x + y$ .

Trả lời:

Câu 21 (1đ):

Để xác định bán kính của chiếc đĩa cổ hình tròn bị vỡ một phần, các nhà khảo cổ lấy ba điểm $A, \, B, \, C$ trên vành đĩa và tiến hành đo đạc thu được kết quả như sau: cạnh $AB\approx 9,5$ cm, $\widehat{ACB}\approx 60^\circ$ .

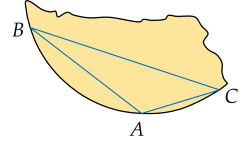
loading...

Tính bán kính của chiếc đĩa. (Làm tròn kết quả đến chữ số thập phân thứ nhất của đơn vị cm)

Trả lời:

Câu 22 (1đ):

Bài học cùng chủ đề

Đề kiểm tra số 1 SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra số 1 SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP