Đề thi tuyển sinh vào lớp 10 THPT Nghệ An năm 2022-2023 SVIP

Hướng dẫn giải:

a) $A =\sqrt{81}-\sqrt{36}+\sqrt{49}$
$=\sqrt{9^2}-\sqrt{6^2}+\sqrt{7^2}$
$=9-6+7$
$=10$
Vậy $A=10$.

b) $P=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}}\right) . \dfrac{x-\sqrt{x}}{2022}$, với $x>0$ và $x \neq 1$.

$P =\left(\dfrac{\sqrt{x}-(\sqrt{x}-1)}{\sqrt{x}(\sqrt{x}-1)}\right) . \dfrac{x-\sqrt{x}}{2022}$ 

$=\left(\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}(\sqrt{x}-1)}\right) . \dfrac{\sqrt{x}(\sqrt{x}-1)}{2022}$

$=\dfrac{1}{\sqrt{x}(\sqrt{x}-1)} . \dfrac{\sqrt{x}(\sqrt{x}-1)}{2022}$

$=\dfrac{1}{2022}$ 

Vậy $P=\dfrac{1}{2022}$.

c) Xét hàm số $y=a x+b$.
Đồ thị hàm số đi qua điểm $M(-1 ; 3)$

$\Rightarrow 3=a .(-1)+b$

$\Leftrightarrow-a+b=3$

Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng $-2$.

$\Rightarrow$ Thay $x=0, y=-2$ vào hàm số ta được:

$-2=a .0+b$

$\Leftrightarrow b=-2$

Thay $b=-2$ vào $(1):-a+(-2)=3 \Leftrightarrow a=-5$

Vậy $a=-5 ; b=-2$.

Hướng dẫn giải:

a) $2 x^2-9 x+10=0$ (1)

Ta có: $\Delta=b^2-4 a c=(-9)^2-4 . 2 . 10=1>0$

$\Rightarrow$ Phương trình (1) có 2 nghiệm phân biệt: $\left[\begin{aligned}x=\dfrac{-b+\sqrt{\Delta}}{2 a}=\dfrac{9+\sqrt{1}}{2.2}=\dfrac{5}{2} \\ x=\dfrac{-b-\sqrt{\Delta}}{2 a}=\dfrac{9-\sqrt{1}}{2.2}=2\end{aligned}\right.$

Vậy tập nghiệm của phương trình (1) là $S=\left\{\dfrac{5}{2} ; 2\right\}$.

b) $x^2+3 x-1=0(2)$

Phương trình (2) có $2$ nghiệm phân biệt $x_1, x_2$, theo định lí Vi-et ta có: $\left\{\begin{aligned}x_1+x_2=-\dfrac{b}{a}=-3 \\ x_1 x_2=\dfrac{c}{a}=-1\end{aligned}\right.$

Ta có $T=\dfrac{3\left|x_1-x_2\right|}{x_1^2 x_2+x_1 x_2^2}=\dfrac{3\left|x_1-x_2\right|}{x_1 x_2\left(x_1+x_2\right)}$

Xét $\left|x_1-x_2\right|^2=x_1^2+x_2^2-2 x_1 x_2=\left(x_1+x_2\right)^2-4 x_1 x_2=(-3)^2-4 .(-1)=13$

$\Leftrightarrow\left|x_1-x_2\right|=\sqrt{13}\left(\right.$ vì $\left.\left|x_1-x_2\right| \geq 0\right)$.

Thay số vào $T$ ta được: $T=\dfrac{3 . \sqrt{13}}{-1 .(-3)}=\sqrt{13}$.

Vậy $T=\sqrt{13}$.

Hướng dẫn giải:

Gọi thời gian dự định để sản xuất $420$ thú nhồi bông của phân xưởng là $x(x>2)$ (giờ).

Theo dự định mỗi giờ phân xưởng sản xuất được $\dfrac{420}{x}$ (thú nhồi bông).

Thời gian thực tế hoàn thành công việc là $x-2$ (giờ).

Thực tế mỗi giờ phân xưởng sản xuất được $\dfrac{420}{x-2}$ (thú nhồi bông).

Theo đề bài thì thực tế mỗi giờ phân xưởng sản xuất thêm $5$ thú nhồi bông so với dự định nên ta có phương trình:

$\dfrac{420}{x-2}-5=\dfrac{420}{x}$

$\Rightarrow  420 x-5 x(x-2)=420(x-2)$

$\Leftrightarrow  5 x^2-10 x-840=0$

$\left[\begin{aligned}  x=-12 \text{ (L)} \\  x=14   \end{aligned}\right.$.

Vậy thời gian dự định của phân xưởng là $14$ giờ.

Hướng dẫn giải:

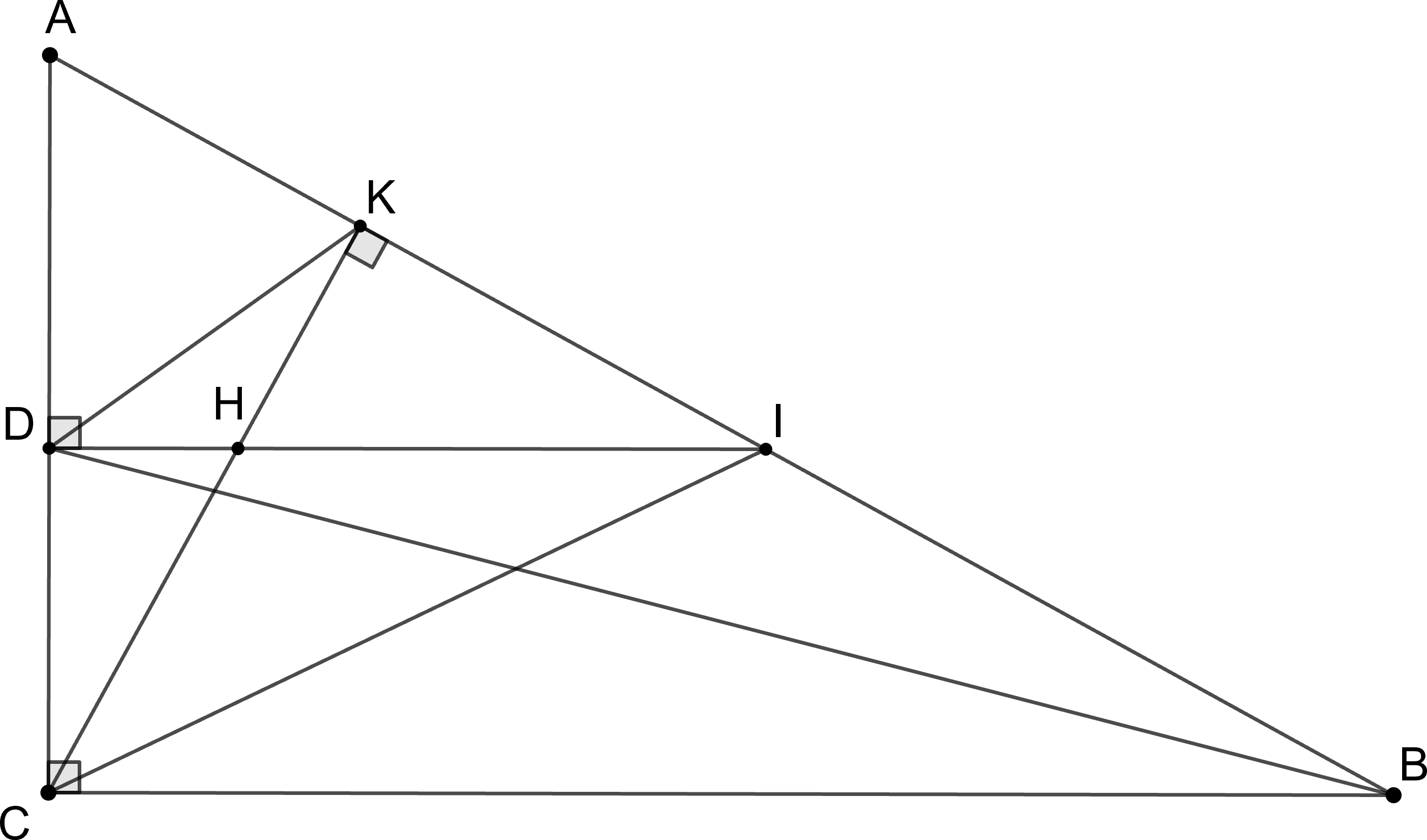
a) Chứng minh $CDKI$ là tứ giác nội tiếp.

Ta có: $D I \perp A C \Rightarrow \widehat{C D I}=90^{\circ}$

$C K \perp A B \Rightarrow \widehat{C K I}=90^{\circ}$

Xét tứ giác $CDKI$ ta có: $\widehat{C D I}=\widehat{C K I}=90^{\circ}$

Mà hai góc này là hai góc có đỉnh kề nhau cùng nhìn cạnh ${CI}$

$\Rightarrow C D K I$ là tứ giác nội tiếp (ĐPCM).

b) Chứng minh: $A D . A C=D H . A B$

$BD$ là phân giác $\widehat{A B C} \Rightarrow \dfrac{B A}{B C}=\dfrac{D A}{D C}$ (t/c tia phân giác) $\Rightarrow \dfrac{A D}{A B}=\dfrac{D C}{B C}$

Xét $\triangle D C H$ và $\triangle C B A$ ta có:

$\widehat{H D C}=\widehat{B C A}=90^{\circ}$

$\widehat{D C H}=\widehat{C B A}(\text { cùng phụ } \widehat{H C B})$

$\Rightarrow \triangle D C H \backsim \triangle C B A(\text { g.g })$

$\Rightarrow \dfrac{D H}{A C}=\dfrac{D C}{B C}$

Từ (1) và (2) 

$\Rightarrow \dfrac{A D}{A B}=\dfrac{D H}{A C} \Rightarrow A D . A C=D H . A B$ (ĐPCM)

c) 

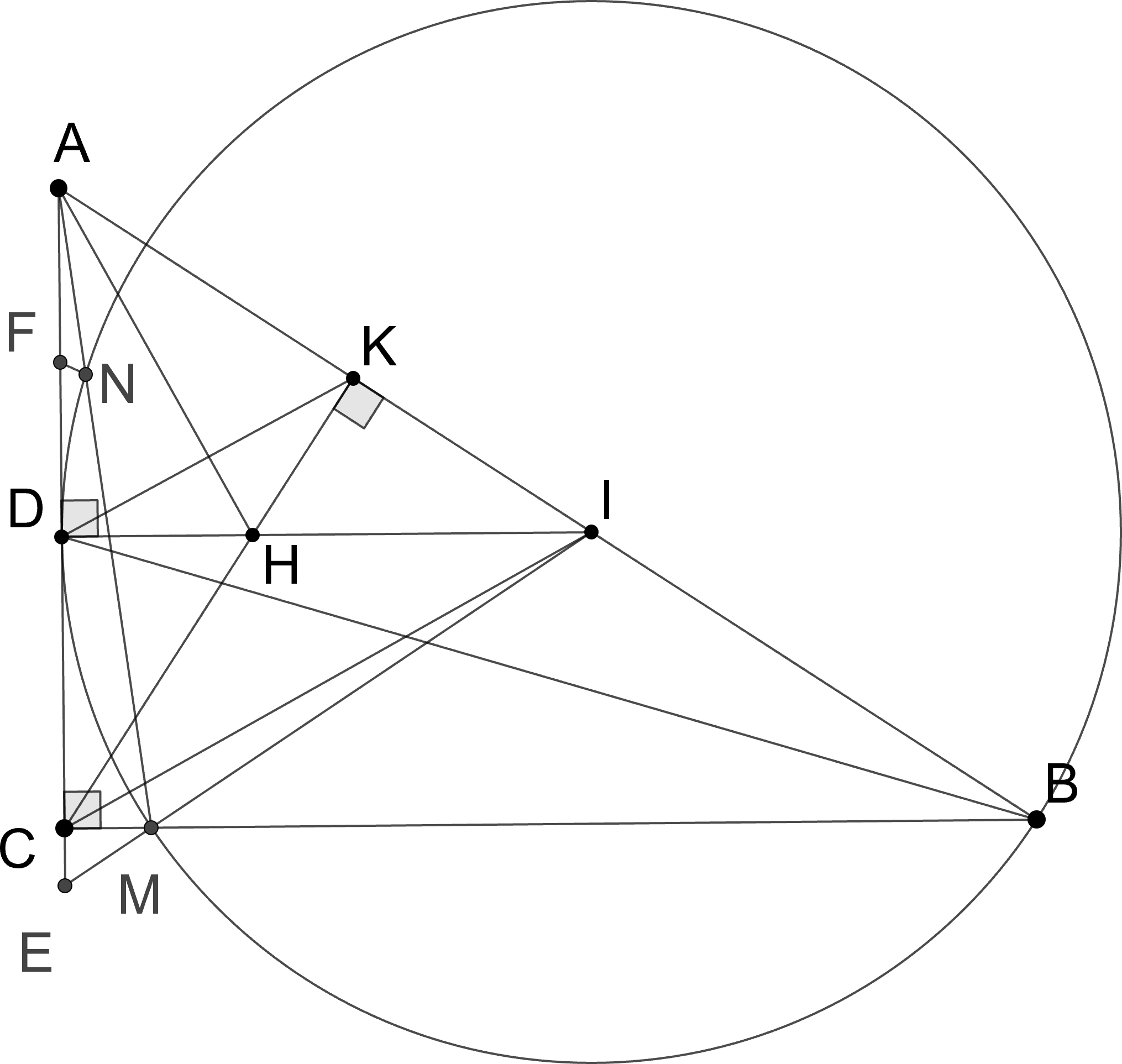
Ta có: $I D \perp A C ; B C \perp A C \Rightarrow I D / / B C$

Gọi $I M \cap A C=\{E\}$

$\triangle I B M$ cân tại ${I} \Rightarrow \widehat{I B M}=\widehat{I M B}$

Mà $\widehat{A I D}=\widehat{I B M}$ (đồng vị)

$\widehat{E I D}  =\widehat{I M B} \text { (so le trong) }$

$\Rightarrow \widehat{A I D} = \widehat{E I D}$

$\Rightarrow I D$ là phân giác $\widehat{A I E}$ mà $I D \perp A E(g t)$

$\Rightarrow \triangle I A E$ cân tại ${I} \Rightarrow \widehat{I A E}=\widehat{I E A}$

Xét $\triangle A D N$ và $\triangle A M D$ có $\widehat{A}$ chung; $\widehat{A D N}=\widehat{A M D}$ (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung ${DN}$ )

$\Rightarrow \triangle A D N \backsim \triangle A M D(g . g)  \Rightarrow A D^2=A N . A M$

Hướng dẫn giải:

Điều kiện $x \neq 0$.

Nhận thấy $V T=\sqrt{x^2+1}+3>0$, với mọi $x \neq 0$.

Khi đó để phương trình có nghiệm thì vế phải của (1) phải lớn hơn $0$.

Hay $\left(\dfrac{1}{x}-3\right)\left(\sqrt{9 x^2-6 x+2}+3\right)>0$

$\Leftrightarrow \dfrac{1}{x}-3>0 \text { do }\left(1 \sqrt{(1-3 x)^2+1}+3>0 \quad \forall x \neq 0\right)$

$\Leftrightarrow \dfrac{1-3 x}{x}>0 \Leftrightarrow 0<x<\dfrac{1}{3} .$

Ta có $\sqrt{x^2+1}+3=\left(\dfrac{1}{x}-3\right)\left(\sqrt{9 x^2-6 x+2}+3\right)$

$\Leftrightarrow x \sqrt{x^2+1}+3 x=(1-3 x)\left(\sqrt{(1-3 x)^2+1}+3\right)$

$\Leftrightarrow x\left(\sqrt{x^2+1}+3\right)=(1-3 x)\left(\sqrt{(1-3 x)^2+1}+3\right) .$

Đặt $1-3 x=t$ điều kiện $t>0$.

Khi đó phương trình trở thành:

$x\left(\sqrt{x^2+1}+3\right)=t\left(\sqrt{t^2+1}+3\right)$

$\Leftrightarrow \sqrt{x^4+x^2}-\sqrt{t^4+t^2}+3 .(x-t)=0$

$\Leftrightarrow \dfrac{\left(\sqrt{x^4+x^2}-\sqrt{t^4+t^2}\right)\left(\sqrt{x^4+x^2}+\sqrt{t^4+t^2}\right)}{\sqrt{x^4+x^2}+\sqrt{t^4+t^2}}+3(x-t)=0$

$\Leftrightarrow \dfrac{\left(x^4-t^4\right)+\left(x^2-t^2\right)}{\left(\sqrt{x^4+x^2} \sqrt{t^4+t^2}\right)}+3(x-t)=0$

$\Leftrightarrow \dfrac{(x-t)(x+t)\left(x^2+t^2\right)+(x-t)(x+t)}{\sqrt{x^4+x^2}+\sqrt{t^4+t^2}}+3(x-t)=0$

$\Leftrightarrow(x-t)\left(\dfrac{(x+t)\left(x^2+t^2+1\right)}{\sqrt{x^4+x^2}+\sqrt{t^4+t^2}}+3\right)=0 \text {. }$

$\Leftrightarrow x-t=0 \quad \text { do } \dfrac{(x+t)\left(x^2+t^2+1\right)}{\sqrt{x^4+x^2}+\sqrt{t^4+t^2}}+3>0$

$\Leftrightarrow x=t$

Suy ra $x=1-3 x \Leftrightarrow x=\dfrac{1}{4}$ (thoả mãn).

Vậy phương trình có nghiệm duy nhất $x=\dfrac{1}{4}$.