Đề tuyển sinh vào lớp 10 tỉnh Hà Tĩnh năm học 2021 - 2022 SVIP

Hướng dẫn giải:

a)

$\begin{aligned}
&P=\sqrt{45}+\sqrt{20}-\sqrt{5} \\
&P=\sqrt{9.5}+\sqrt{4.5}-\sqrt{5} \\
&P=3 \sqrt{5}+2 \sqrt{5}-\sqrt{5}=4 \sqrt{5} .
\end{aligned}$
Vậy $P=4 \sqrt{5}$.
b) $Q=\left(\dfrac{1}{2 \sqrt{x}+1}+\dfrac{1}{2 \sqrt{x}-1}\right): \dfrac{1}{1-4 x}$ vơi $x \geq 0, x \neq \dfrac{1}{4}$.
$\begin{aligned}
&Q=\left(\dfrac{1}{2 \sqrt{x}+1}+\dfrac{1}{2 \sqrt{x}-1}\right): \dfrac{1}{1-4 x} \\
&Q=\dfrac{2 \sqrt{x}-1+2 \sqrt{x}+1}{(2 \sqrt{x}+1)(2 \sqrt{x}-1)}: \dfrac{1}{1-4 x} \\
&Q=\dfrac{4 \sqrt{x}}{4 x-1}: \dfrac{1}{1-4 x} \\
&Q=\dfrac{4 \sqrt{x}}{4 x-1} \cdot(1-4 x)=\dfrac{4 \sqrt{x}}{-(1-4 x)} \cdot(1-4 x)=-4 \sqrt{x}
\end{aligned}$
Vậy $Q=-4 \sqrt{x}$, với $x \geq 0, x \neq \dfrac{1}{4}$.

Hướng dẫn giải:

Hai đường thẳng $(d)$ và $\left(d_{1}\right)$ song song với nhau khi và chỉ khi
$$
\left\{\begin{array} { l } 
{ m = 1 } \\
{ 3 m + 2 \neq 1 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
m=1 \\
m \neq-\dfrac{1}{3}
\end{array} \Leftrightarrow m=1 .\right.\right.
$$
Vậy với $m=1$ thì $(d)$ và $\left(d_{1}\right)$ song song với nhau.

Hướng dẫn giải:

a) Giải phương trình với $m=1$.
Với $m=1$, phương trình đã cho trở thành $x^{2}-4 x+1=0$.
Ta có $\Delta^{\prime}=2^{2}-1=3>0$ nên phương trình có 2 nghiệm phân biệt $\left[\begin{array}{l}x_{1}=\dfrac{-b^{\prime}+\sqrt{\Delta^{\prime}}}{a}=2+\sqrt{3} \\ x_{2}=\dfrac{-b^{\prime}-\sqrt{\Delta^{\prime}}}{a}=2-\sqrt{3}\end{array}\right.$.
Vậy khi $m=1$ tập nghiệm của phương trình là $S=\{2 \pm \sqrt{3}\}$.
b) Ta có: $\Delta^{\prime}=(m+1)^{2}-m^{2}=2 m+1$.
Để phương trình đã cho có 2 nghiệm $x_{1}, x_{2}$ thì $\Delta^{\prime} \geq 0 \Leftrightarrow 2 m+1 \geq 0 \Leftrightarrow m \geq-\dfrac{1}{2}$.
Khi đó áp dụng định li Vi-ét ta có: $\left\{\begin{array}{l}x_{1}+x_{2}=2(m+1) \\ x_{1} x_{2}=m^{2}\end{array}\right.$.
Theo bài ra ta có:
$\begin{aligned}
&x_{1}^{2}+x_{2}^{2}+6=4 x_{1} x_{2} \\
&\Leftrightarrow\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}+6=4 x_{1} x_{2} \\
&\Leftrightarrow\left(x_{1}+x_{2}\right)^{2}-6 x_{1} x_{2}+6=0 \\
&\Leftrightarrow 4(m+1)^{2}-6 m^{2}+6=0 \\
&\Leftrightarrow-2 m^{2}+8 m+10=0\ (1)
\end{aligned}$
Ta có $a-b+c=-2-8+10=0$ nên phương trình có 2 nghiệm phân biệt
$\left[\begin{array}{l}
m_{1}=-1(\text{loại}) \\
m_{2}=-\dfrac{c}{a}=-\dfrac{10}{-2}=5(tm)
\end{array}\right.$
Vậy có 1 giá trị của $m$ thỏa mãn là $m=5$.

Hướng dẫn giải:

Giả sử giả tiền điện hàng tháng được tính theo bậc thang như sau:
Bậc 1: Từ $1 kWh$ đến $100 kWh$ thì giá điện là: $1500 đ / kWh$
Bậc 2: Từ $101 kWh$ đến $150 kWh$ thì giá điện là: $2000 đ / kWh$
Bậc 3: Từ $151 kWh$ trở lên thì giá điện là: $4000 đ / kWh$
(Ví dụ: Nếu dùng $170 kWh$ thi có $100 kWh$ tính theo giá bậc 1, có $50 kWh$ tính theo giá bâck 2 và có $20 k W h$ tính theo giá bậc 3 ).
Tháng 4 năm 2021 tổng số tiền điện của nhà bạn $A$ và nhà bạn $B$ là $560000 ~d$. So với tháng 4 thì tháng 5 tiền điện của nhà bạn $A$ tăng $30 \%$, nhà bạn $B$ tăng $20 \%$, do dó tổng số tiền điện của cả hai nhà trong tháng 5 là $701000 ~d$. Hỏi tháng 4 nhà bạn $A$ phải trả bao nhiêu tiền điện và dùng hết bao nhiêu $k W h$ ? (biết rằng số tiền điện ở trên không tính thuế giá trị gia tăng).
Gọi số tiền điện nhà bạn $A$ phải trả trong tháng 4 là $x(x>0)$ (dồng)
Số tiền điện nhà bạn $B$ phải trà trong tháng 4 là $y(y>0)$ (dồng)
Theo bài ta có tổng số tiền điện trong tháng 4 nhà bạn $A$ và nhà bạn $B$ phải trả là 560000 nên ta có phương trình $x+y=560000$ (1)
Số tiền điện trong tháng 5 nhả bạn $A$ phải trả là $x+30 \% x=1,3 x$ (đồng)
Số tiền điện trong tháng 5 nhà bạn $B$ phải trả là: $y+20 \% y=1,2 y$ (đồng)
Theo bài ta có tổng số tiền điện trong tháng 5 nhà bạn $A$ và nhà bạn $B$ phải trả là 701000 nên ta có phương trình: $1,3 x+1,2 y=701000$ (2)

Từ (1) và (2) ta có hệ phương trình:
$\left\{\begin{array}{l}
x+y=560000 \\
1,3 x+1,2 y=701000
\end{array}\right.$
$\Leftrightarrow\left\{\begin{array} { l } 
{ x = 5 6 0 0 0 0 - y } \\
{ 1 , 3 ( 5 6 0 0 0 0 - y ) + 1 , 2 y = 7 0 1 0 0 0 }
\end{array}\right.$

$\Leftrightarrow \left\{\begin{array}{l}
x=560000-y \\
728000-0,1 y=701000
\end{array}\right.$

$\Leftrightarrow\left\{\begin{array} { l } 
{ x = 5 6 0 0 0 0 - y } \\
{ 0 , 1 y = 2 7 0 0 0 }
\end{array}\right.$

$\Leftrightarrow \left\{\begin{array}{l}
x=290000 \\
y=270000
\end{array}\right.$
Vậy số tiền điện nhà bạn $A$ phải trả trong tháng 4 là 290000 đồng.
Nhận thấy: $290000=100.1500+50.2000+10.4000$
Vậy số điện nhà bạn $A$ dùng trong tháng 4 là $100+50+10=160(k W h)$.

Hướng dẫn giải:

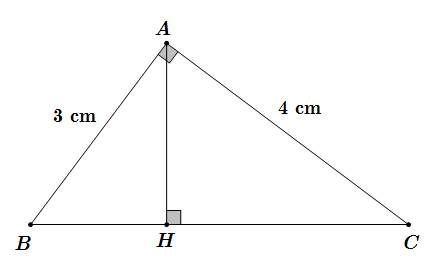
Áp dụng hệ thức lượng trong tam giác vuông $A B C$ ta có:
$\begin{aligned}
& \dfrac{1}{A H^{2}}=\dfrac{1}{A B^{2}}+\dfrac{1}{A C^{2}} \\
\Rightarrow & \dfrac{1}{A H^{2}}=\dfrac{1}{3^{2}}+\dfrac{1}{4^{2}} \\
\Rightarrow & \dfrac{1}{A H^{2}}=\dfrac{1}{9}+\dfrac{1}{16} \\
\Rightarrow & \dfrac{1}{A H^{2}}=\dfrac{25}{144} \\
\Rightarrow & A H=\dfrac{144}{25} \\
\Rightarrow & A H=\dfrac{12}{5}(~cm)
\end{aligned}$
Áp dụng định li Pytago trong tam giác vuông $A H C$ ta có:
$\begin{aligned}
&A C^{2}=A H^{2}+H C^{2} \\
&\Rightarrow 4^{2}=\left(\dfrac{12}{5}\right)^{2}=H C^{2} \\
&\Rightarrow H C^{2}=16-\dfrac{144}{25} \\
&\Rightarrow H C^{2}=\dfrac{256}{25} \\
&\Rightarrow H C=\dfrac{16}{5}(~cm)
\end{aligned}$
Vì tam giác $A H C$ vuông tại $H$ nên $S_{\triangle H H}=\dfrac{1}{2} A H \cdot H C=\dfrac{1}{2} \cdot \dfrac{12}{5} \cdot \dfrac{16}{5}=\dfrac{96}{25}\left(~cm^{2}\right)$.

Hướng dẫn giải:

a) Chứng minh $\widehat{C A E}=\widehat{B C E}$.
Vì $E$ là diểm chính giữa của cung nhỏ $B C$ nên $\operatorname{sdc} B E=\operatorname{sdc} C E$.
$\Rightarrow \widehat{C A E}=\widehat{B C E}$ (trong một đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau).
b) Gọi $M$ là điểm trên cạnh $A C$ sao cho $E M=E C(M$ khác $C)$; $N$ là giao điểm của $B M$ với đường tròn tâm $O(N$ khác $B)$. Gọi $I$ là giao diểm của $B M$ với $A E ; K$ là giao diểm của $A C$ với $E N$. Chứng minh tứ giác EKMI nội tiếp.
Vì $E M=E C(g t)$, mà $E B=E C$ (do $s d c E B=s d c E C) \Rightarrow E B=E M$.
$\Rightarrow \triangle E B M$ cân tại $M \Rightarrow \widehat{E B M}=\widehat{E M B}$ (2 góc ở đáy).
Ta có: $\widehat{E B M}+\widehat{E C N}=180^{\circ}$ ( 2 góc đối diện của tứ giác nội tiếp $B E C N$ )
$$
\begin{aligned}
&\widehat{E M B}+\widehat{E M N}=180^{\circ} \text { (kề bù) } \\
&\Rightarrow \widehat{E C N}=\widehat{E M N} .
\end{aligned}
$$
Lại có $\widehat{E N C}=\widehat{E N M}$ ( 2 góc nội tiểp chắn hai cung bằng nhau)
$$
\begin{aligned}
&\Rightarrow \widehat{E C N}+\widehat{E N C}=\widehat{E M N}+\widehat{E N M} \\
&\Rightarrow 180^{\circ}-\widehat{C E N}=180^{\circ}-\widehat{M E N} \\
&\Rightarrow \widehat{C E N}=\widehat{M E N}
\end{aligned}
$$
$\Rightarrow E K$ là phân giác của $\widehat{M E C}$.
Mà tam giác $E M C$ cân tại $E(E M=E C)$ nên $E K$ đồng thời là đường cao $\Rightarrow E K \perp M C$.
$\Rightarrow \widehat{E K M}=90^{\circ} .$ $\Rightarrow \widehat{E A K}+\widehat{A E K}=90^{\circ}$. Mà $\widehat{E A K}=\widehat{E A C}=\widehat{B N E}(2$ góc nội tiểp chắn hai cung bẳng nhau $)$ $\Rightarrow \widehat{B N E}+\widehat{A E K}=90^{\circ} \Rightarrow \widehat{B N I}+\widehat{I E N}=90^{\circ} \Rightarrow \widehat{E I N}$ vuông tại $I .$ $\Rightarrow \widehat{E I N}=90^{\circ} \Rightarrow \widehat{E I M}=90^{\circ} .$ $\Rightarrow \widehat{B N E}+\widehat{A E K}=90^{\circ} \Rightarrow \widehat{B N I}+\widehat{I E N}=90^{\circ} \Rightarrow \widehat{E I N}$ vuông tại $I$.
$\Rightarrow \widehat{E I N}=90^{\circ} \Rightarrow \widehat{E I M}=90^{\circ}$.
Xét tứ giác $E K M I$ có: $\widehat{E K M}+\widehat{E I M}=90^{\circ}+90^{\circ}=180^{\circ}$.
Vậy EKMI là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng $180^{\circ}$ ).
Câu 7. (1,0 điểm) Cho các số thực không âm $a, b, c$ thỏa mãn: $a+b+c=2021$. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: $p=\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}$.
Ta có: $P=\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}$
$\Rightarrow P^{2}=(\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a})^{2} \leq 3(a+b+b+c+c+a)=6.2021=12126$ (BĐT
Buniacopxki)
$\Rightarrow P^{2} \leq 12126 \Leftrightarrow P \leq \sqrt{12126}$
Dấu "=" xảy ra $\Leftrightarrow 2021-c=2021-a=a+c \Leftrightarrow\left\{\begin{array}{l}a=c \\ 2021-a=2 a\end{array} \Leftrightarrow a=c=\dfrac{2021}{3}=b\right.$.

Hướng dẫn giải:

Ta có: $P=\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}$
$\Rightarrow P^{2}=(\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a})^{2} \leq 3(a+b+b+c+c+a)=6.2021=12126$ (BĐT
Buniacopxki)
$$
\Rightarrow P^{2} \leq 12126 \Leftrightarrow P \leq \sqrt{12126}
$$
Dấu "=" xảy ra $\Leftrightarrow 2021-c=2021-a=a+c \Leftrightarrow\left\{\begin{array}{l}a=c \\ 2021-a=2 a\end{array} \Leftrightarrow a=c=\dfrac{2021}{3}=b\right.$.
Vậy $P_{\max }=\sqrt{12126} \Leftrightarrow a=b=c=\dfrac{2021}{3}$.