Phần tự luận (7 điểm) SVIP

Hướng dẫn giải:

​$A=2.\sqrt{80}-2.\sqrt{245}+2\sqrt{180}$

$A=2.\sqrt{16.5}-2.\sqrt{49.5}+2\sqrt{36.5}$

$A=8\sqrt{5}-14\sqrt{5}+12\sqrt{5}$

$A=6\sqrt{5}$.

Hướng dẫn giải:

a. Rút gọn $P$.

$P=\dfrac{x}{\sqrt{x}(\sqrt{x}-1)}+\dfrac{2}{\sqrt{x}(\sqrt{x}+2)}+\dfrac{x+2}{\sqrt{x}(\sqrt{x}-1)(\sqrt{x}+2)}$

$=\dfrac{x(\sqrt{x}+2)+2(\sqrt{x}-1)+x+2}{\sqrt{x}(\sqrt{x}-1)(\sqrt{x}+2)}=\dfrac{x\sqrt{x}+2x+2\sqrt{x}-2+x+2}{\sqrt{x}(\sqrt{x}-1)(\sqrt{x}+2)}$

$=\dfrac{x\sqrt{x}+2x+2\sqrt{x}+x}{\sqrt{x}(\sqrt{x}-1)(\sqrt{x}+2)}=\dfrac{\sqrt{x}(\sqrt{x}+1)(\sqrt{x}+2)}{\sqrt{x}(\sqrt{x}-1)(\sqrt{x}+2)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}$.

b. Tính $P$ khi $x=3+2\sqrt{2}$.

Xét $x=3+2\sqrt{2}$ (thỏa mãn điều kiện)

$\sqrt{x}=\sqrt{2+2\sqrt{2}+1}=\sqrt{(\sqrt{2}+1)^2}=\sqrt{2}+1$.

Khi đó: 

$P=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{\sqrt{2}+1+1}{\sqrt{2}+1-1}=\dfrac{\sqrt{2}+2}{\sqrt{2}}=1+\sqrt{2}$.

Hướng dẫn giải:

Gọi số học sinh dự thi của trường A và trường B lần lượt là $x$ và $y$ (học sinh). Điều kiện: $x,y\in \mathbb{N}^*.$

Do cả hai trường có $840$ học sinh thi đỗ vào lớp $10$ và đạt tỉ lệ thi đỗ là $84\%$ nên ta có phương trình:

$84\%.(x+y)=840$ hay $x+y=1\,000$ (1)

Vì trường A tỉ lệ thi đỗ là $80\%$, trường B tỉ lệ thi đỗ là $90\%$ nên ta có phương trình:

$80\%.x+90\%.y=840$

$0,8x+0,9y=840$

$8x+9y=8\,400$ (2)

Từ $(1)$ và $(2)$ ta có hệ phương trình:

$\left\{ \begin{aligned}& x+y=1\,000 \\& 8x+9y=8\,400 \\\end{aligned} \right.$

$\left\{ \begin{aligned}& 9x+9y=9\,000 \\& 8x+9y=8\,400 \\\end{aligned} \right.$

$\left\{ \begin{aligned}& x=600 \\& y=400 \\\end{aligned} \right.$ (thỏa mãn điều kiện).

Vậy số học sinh dự thi của trường A và trường B lần lượt là $600$ và $400$ (học sinh).

Hướng dẫn giải:

a)

Xét $\Delta ABC$ vuông tại $A$, ta có:

$\sin \widehat{B}=\dfrac{AC}{BC}=\dfrac{12}{320}=\dfrac{3}{80}$ 

Suy ra $\widehat{B} \approx 2^\circ 9'$.

Vậy góc nghiêng là $2^\circ 9'$.

b)

Xét $\Delta ABC$ vuông tại $A$, ta có:

$BC=\dfrac{AC}{\sin \widehat{B}}=\dfrac{12}{\sin 5^\circ}\approx 137,7$ km.

Vậy phải bắt đầu cho máy bay hạ cánh khi cách sân bay $137,7$ km.

Hướng dẫn giải:

​Gọi $x$ là số ti vi mà cửa hàng đặt mỗi lần ($x \in [1; 2\,500]$, đơn vị cái).

Số lượng ti vi trung bình gửi trong kho là $\dfrac{x}{2}$ nên chi phí lưu kho tương ứng là $10 . \dfrac{x}{2} = 5x$ $(\$)$

Số lần đặt hàng mỗi năm là $\dfrac{2\,500}{x}$ và chi phí đặt hàng là:

$\dfrac{2\,500}{x} . (20 + 9x)$ $(\$)$

Khi đó chi phí mà cửa hàng phải trả là:

$C(x) = \dfrac{2\,500}{x} . (20 + 9x) + 5x = 5x + \dfrac{50\,000}{x} + 22\,500$

Ta có $5x+\dfrac{50\,000}{x} \le 2 \sqrt{5x.\dfrac{50\,000}{x}}=1\,000$.

Suy ra $C(x) \le 23\,500$. Dấu $"="$ xảy ra khi $5x=\dfrac{50\,000}{x}$, khi đó $x=100$.

Vậy mỗi năm, cửa hàng nên đặt $100$ cái ti vi để chi phí hàng tồn kho là nhỏ nhất.

Hướng dẫn giải:

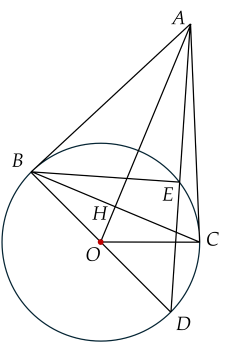
a) Xét đường tròn $(O)$ có: $AB$, $AC$ lần lượt là tiếp tuyến tại $B,\,C$ nên $AB = AC$ (tính chất hai tiếp tuyến cắt nhau) .

Suy ra $A$ thuộc đường trung trực của $BC$.

Mà $OB = OC = R$ nên $O$ thuộc đường trung trực của $BC$

Do đó $OA$ là đường trung trực của $BC$ nên $OA \bot BC$ tại $H$.

b) Xét tam giác $BED$ có $OE$ là trung tuyến. Mặt khác $OE=\dfrac{BD}{2}$ nên tam giác $BED$ vuông tại $E$.

Xét $\Delta ABE$ và $\Delta ABD$ có

$\widehat{BAD}$: góc chung

$\widehat{BEA}=\widehat{DBA}=90^\circ$

Suy ra $\Delta ABE \sim \Delta ADB$ (g.g)

Khi đó $\widehat{ABE}=\widehat{ADB}$ (hai góc tương ứng)

và $\dfrac{AB}{AD}=\dfrac{AE}{AB}$ hay $AB^2=AD.AE$ (đpcm).

c) Xét tam giác vuông $AOB$ có:

$\cos {\widehat{AOB}}=\dfrac{OB}{OA}=\dfrac{1}{\sqrt{6}+\sqrt{2}}$.

Suy ra $\widehat{AOB}=75^\circ$. Do đó $\widehat{BOC}=150^\circ$.

Khi đó $\widehat{COD}=30^\circ$. 

Diện tích hình quạt giới hạn bởi bán kính $OC$, $OD$ và cung nhỏ $CD$ là:

$S=\dfrac{\pi R^2.30}{360}=\dfrac{\pi R^2}{12}$ (đvdt).

Vậy diện tích hình quạt giới hạn bởi bán kính $OC$, $OD$ và cung nhỏ $CD$ là $\dfrac{\pi R^2}{12}$ (đvdt).