a) x2-36=0 b) x2 -10x +25=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\left(3x-1\right)\left(x+2\right)-\left(x+2\right)^2\)
\(=\left(3x^2+6x-x-2\right)-\left(x+2\right)^2\)
\(=\left(3x^2+5x-2\right)-\left(x^2+4x+4\right)\)
\(=3x^2+5x-2-x^2-4x-4\)
\(=2x^2+x-6\)
b) \(\left(x-1\right)\left(x+1\right)-\left(x^2-2x+1\right)\)
\(=\left(x^2-1\right)-\left(x^2-2x+1\right)\)
\(=x^2-1-x^2+2x-1\)
\(=2x-2\)
c) \(\left(x-4\right)\left(4+x\right)+2x\left(x-3\right)\)
\(=\left(x-4\right)\left(x+4\right)+2x\left(x-3\right)\)
\(=\left(x^2-16\right)+2x^2-6x\)
\(=x^2-16+2x^2-6x\)
\(=3x^2-6x-16\)
d) \(\left(x-1\right)\left(x^2-1\right)+\left(x+2\right)^3\)
\(=\left(x^3-x-x^2+1\right)+\left(x^3+6x^2+12x+8\right)\)
\(=x^3-x-x^2+1+x^3+6x^2+12x+8\)
\(=2x^3+5x^2+11x+9\)
e) \(\left(2x-1\right)^2-\left(2x-5\right)\left(x+5\right)\)
\(=\left(4x^2-4x+1\right)-\left(2x^2+10x-5x-25\right)\)
\(=\left(4x^2-4x+1\right)-\left(2x^2+5x-25\right)\)
\(=4x^2-4x+1-2x^2-5x+25\)
\(=2x^2-9x+26\)
f) \(\left(3x+1\right)^2-\left(x^2-1\right)\left(x^2+2\right)\)
\(=\left(9x^2+6x+1\right)-\left(x^4+2x^2-x^2-2\right)\)
\(=\left(9x^2+6x+1\right)-\left(x^4+x^2-2\right)\)
\(=9x^2+6x+1-x^4-x^2+2\)
\(=-x^4+8x^2+6x+3\)
g) \(\left(x^2+1\right)^2-\left(x^2-1\right)\left(x^2+2\right)\)
\(=\left(x^4+2x^2+1\right)-\left(x^4+2x^2-x^2-2\right)\)
\(=\left(x^4+2x^2+1\right)-\left(x^4+x^2-2\right)\)
\(=x^4+2x^2+1-x^4-x^2+2\)
\(=x^2+3\)
h) \(\left(2x^2-4\right)^2-\left(2x^2+4\right)^2\)
\(=\left(4x^4-16x^2+16\right)-\left(4x^4+16x^2+16\right)\)
\(=4x^4-16x^2+16-4x^4-16x^2-16\)
\(=-32x^2\)

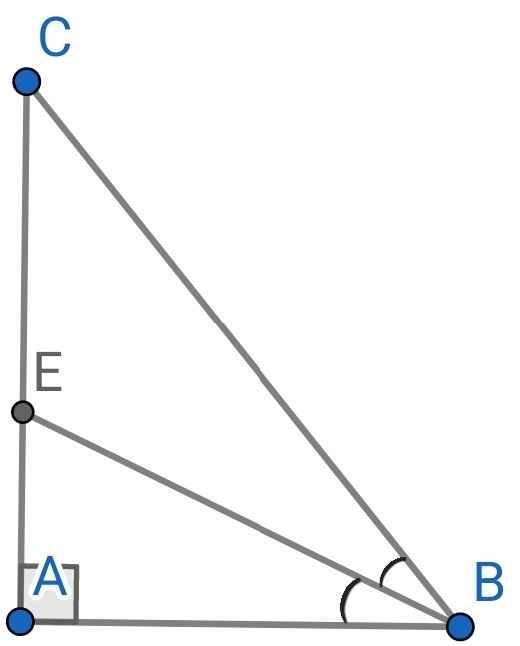 ∆ABC có BE là đường phân giác (gt)
∆ABC có BE là đường phân giác (gt)
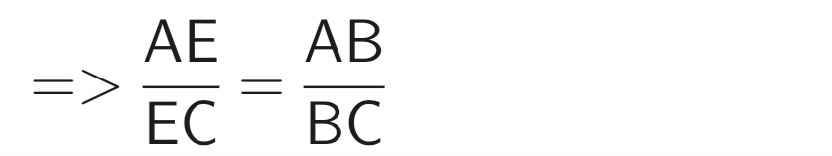
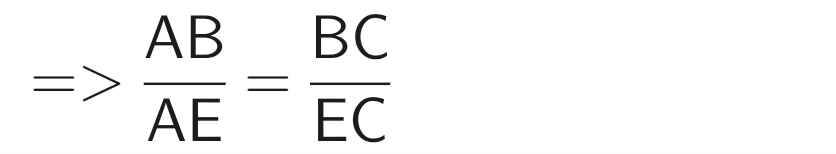
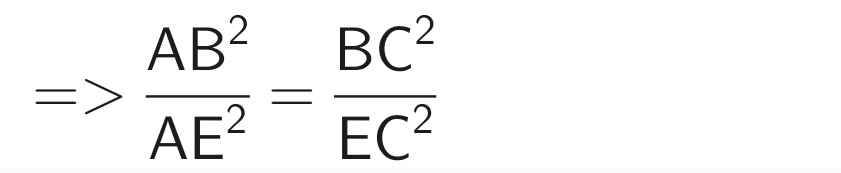 ∆ABC vuông tại A (gt)
∆ABC vuông tại A (gt)
⇒ BC² = AB² + AC² (Pythagore)
⇒ BC² - AB² = AC²
= (3 + 5)²
= 64
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

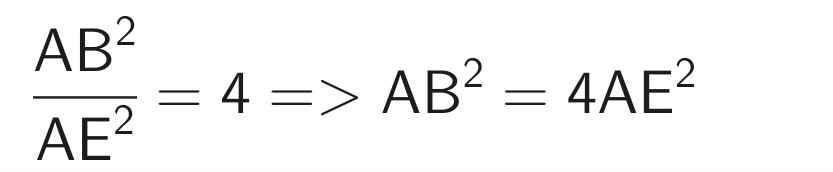

 Ta có:
Ta có:
BC² = AB² + AC² (Pythagore)
= 6² + 64
= 100
⇒ BC = 10
vì BE là đường phân giác của tam giác ABC nên ta có:
\(\dfrac{AE}{EC}=\dfrac{AB}{BC}=\dfrac{3}{5}\)
\(BC=\dfrac{5}{3}AB\)
áp dụng định lý pythagore vào tam giác ABC ta được:
\(AC^2=AB^2+BC^2\)
tổng độ dài đoạn AC là: 3 + 5 = 8
\(AB^2+BC^2=8^2\\ AB^2+\left(\dfrac{5}{3}AB\right)^2=64\\ AB^2+\dfrac{25}{9}AB^2=64\\ AB^2\cdot\left(1+\dfrac{25}{9}\right)=64\\ AB^2\cdot\dfrac{34}{9}=64\\ AB^2=64:\dfrac{34}{9}=64\cdot\dfrac{9}{34}\\ AB^2=\dfrac{576}{34}\\ AB=\sqrt{\dfrac{576}{34}}\text{≈}4,11\)
độ dài đoạn BC là:
BC² = AC² - AB²
BC² = 64 - 16,8921
BC² = 47,1079
BC = \(\sqrt{47,1079}\) ≈ 6,86
VẬY AB = 4,11; BC =6,86

Đa thức $2x^4-21x^2+1$ không phân tích thành nhân tử bạn nhé.

Xét ΔABC vuông tại A có \(sinACB=\dfrac{AB}{BC}\)
=>\(\dfrac{5}{BC}=sin30=\dfrac{1}{2}\)
=>BC=10(cm)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{10^2-5^2}=5\sqrt{3}\left(cm\right)\)

Lời giải:
$A=(4a^2+4b^2+c^2+8ab-4ac-4bc)+(4b^2+4c^2+a^2+8bc-4ab-4ac)+(4c^2+4a^2+b^2+8ac-4bc-4ab)$
$=6(a^2+b^2+c^2)=6m$

\(\dfrac{7^{49}-7^{48}}{7^{48}}\)
\(=\dfrac{7^{49}}{7^{48}}-\dfrac{7^{48}}{7^{48}}\)
\(=7-1\)
\(=6\)
\(\dfrac{7^{49}-7^{48}}{7^{48}}\)
\(=\dfrac{7^{48}\cdot7-7^{48}}{7^{48}}\)
\(=\dfrac{7^{48}\left(7-1\right)}{7^{48}}\)
\(=7-1\)
\(=6\)

13)
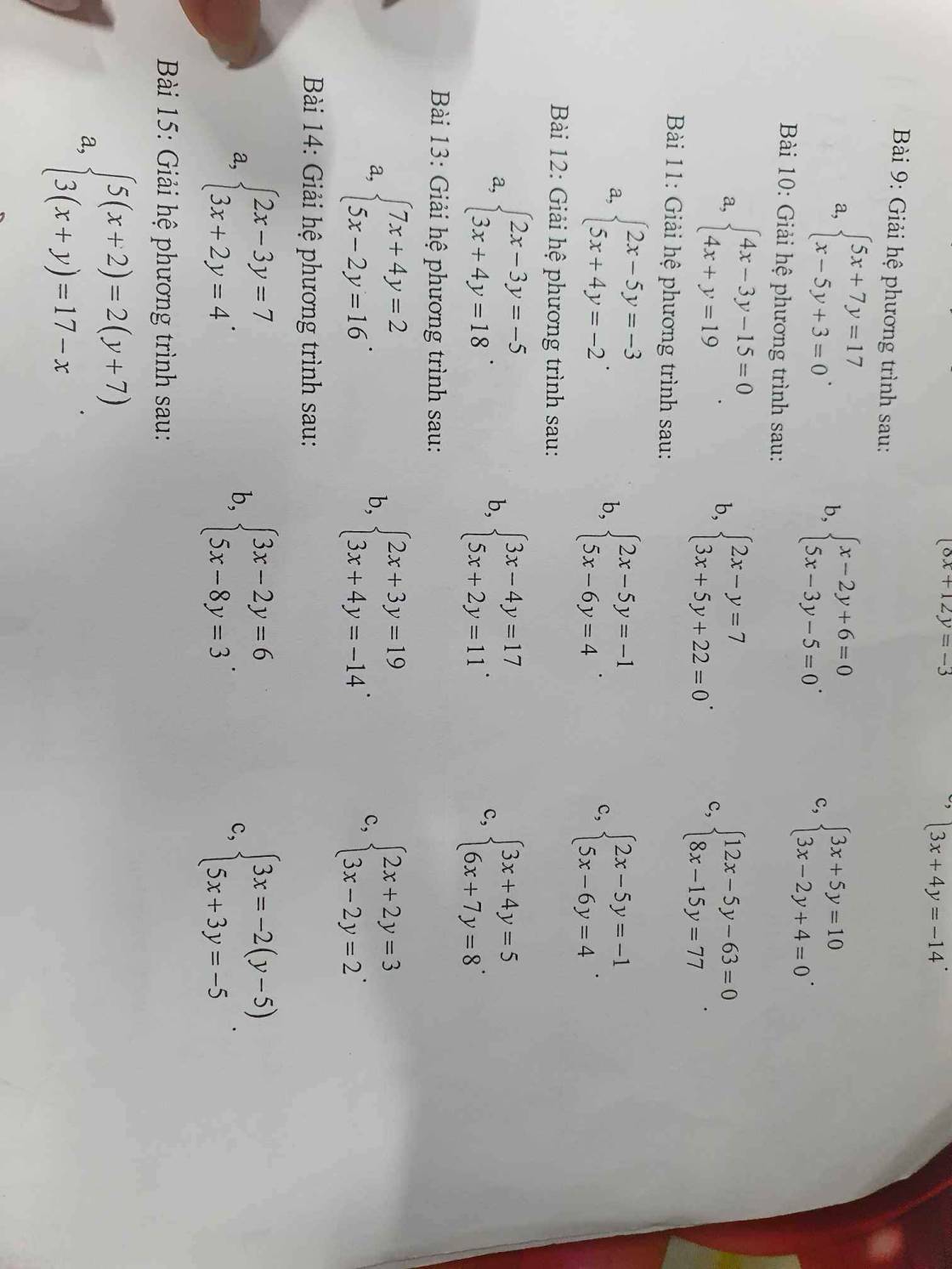
a) \(\left\{{}\begin{matrix}7x+4y=2\\5x-2y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7x+4y=2\\10x-4y=32\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x+4y=2\\17x=34\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7\cdot2+4y=2\\x=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4y=2-14\\x=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4y=-12\\x=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=2\end{matrix}\right.\)
Vậy: ....
b) \(\left\{{}\begin{matrix}2x+3y=19\\3x+4y=-14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x+9y=57\\6x+8y=-28\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+3y=19\\y=85\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+3\cdot85=19\\y=85\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x=19-255\\y=85\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=-236\\y=85\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-118\\y=85\end{matrix}\right.\)
Vậy: ....
c) \(\left\{{}\begin{matrix}2x+2y=3\\3x-2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x=5\\3x-2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\3\cdot1-2y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\-2y=2-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\-2y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{1}{2}\end{matrix}\right.\)
Vậy: ....
15)
a) \(\left\{{}\begin{matrix}5\left(x+2\right)=2\left(y+7\right)\\3\left(x+y\right)=17-x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x+10=2y+14\\3x+3y=17-x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x-2y=14-10\\3x+3y+x=17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x-2y=4\\4x+3y=17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}15x-6y=12\\8x+6y=34\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x-2y=4\\23x=46\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5\cdot2-2y=4\\x=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2y=6\\x=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=3\\x=2\end{matrix}\right.\)
vậy: ...

Do đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng -2,5 nên đi qua điểm (-2,5; 0)
Thay tọa độ điểm (-2,5; 0) vào hàm số, ta có:
2.(-2,5) + b = 0
-5 + b = 0
b = 0 + 5
b = 5
Vậy hàm số cần xác định là: y = 2x + 5
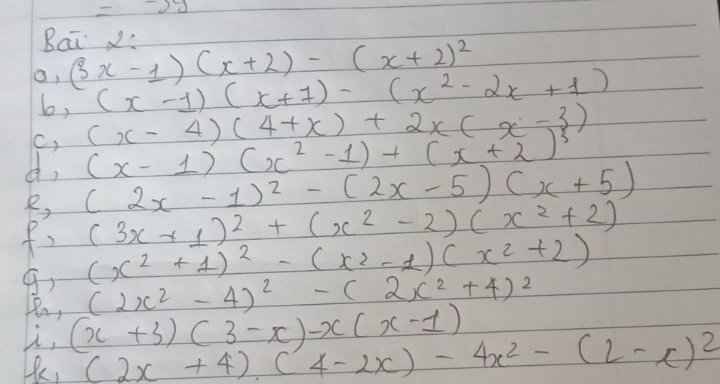
a) \(x^2-36=0\)
\(\Leftrightarrow x^2-6^2=0\)
\(\Leftrightarrow\left(x-6\right)\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-6=0\\x+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-6\end{matrix}\right.\)
Vậy: ...
b) \(x^2-10x+25=0\)
\(\Leftrightarrow x^2-2\cdot x\cdot5+5^2=0\)
\(\Leftrightarrow\left(x-5\right)^2=0\)
\(\Leftrightarrow x-5=0\)
\(\Leftrightarrow x=5\)
Vậy: ...
a) \(x^2-36=0\)
\(\Leftrightarrow x^2=36\)
\(\Leftrightarrow x^2=\left(\pm6\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-6\end{matrix}\right.\)
Vậy \(x\in\left\{6;-6\right\}\)
b) \(x^2-10x+25=0\)
\(\Leftrightarrow x^2-2.x.5+5^2=0\)
\(\Leftrightarrow\left(x-5\right)^2=0\)
\(\Leftrightarrow x-5=0\)
\(\Leftrightarrow x=5\)
Vậy \(x=5\)